Metric space
In mathematics, a metric space is a set together with a notion of distance between its elements, usually called points.
[1] Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry.
[3] Many of the basic notions of mathematical analysis, including balls, completeness, as well as uniform, Lipschitz, and Hölder continuity, can be defined in the setting of metric spaces.
We can measure the distance between two such points by the length of the shortest path along the surface, "as the crow flies"; this is particularly useful for shipping and aviation.
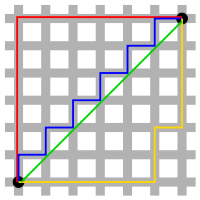
and can be thought of as the distance you need to travel along horizontal and vertical lines to get from one point to the other, as illustrated at the top of the article.
This distance does not have an easy explanation in terms of paths in the plane, but it still satisfies the metric space axioms.
It can be thought of similarly to the number of moves a king would have to make on a chess board to travel from one point to another on the given space.
Arthur Cayley, in his article "On Distance", extended metric concepts beyond Euclidean geometry into domains bounded by a conic in a projective space.
[8][9][10] Fréchet's work laid the foundation for understanding convergence, continuity, and other key concepts in non-geometric spaces.
Metric spaces continue to play a crucial role in the study of abstract mathematical concepts.
[a] The Nagata–Smirnov metrization theorem gives a characterization of metrizability in terms of other topological properties, without reference to metrics.
By the triangle inequality, any convergent sequence is Cauchy: if xm and xn are both less than ε away from the limit, then they are less than 2ε away from each other.
For example, in abstract algebra, the p-adic numbers are defined as the completion of the rationals under a different metric.
In other words, uniform continuity cannot distinguish any non-topological features of compact metric spaces.
[14] For example, a curve in a metric space is rectifiable (has finite length) if and only if it has a Lipschitz reparametrization.
If the metric space M is compact, the result holds for a slightly weaker condition on f: a map
An unusual property of normed vector spaces is that linear transformations between them are continuous if and only if they are Lipschitz.
On a connected Riemannian manifold, one then defines the distance between two points as the infimum of lengths of smooth paths between them.
One application of metric measure spaces is generalizing the notion of Ricci curvature beyond Riemannian manifolds.
On the other hand, in the worst case the required distortion (bilipschitz constant) is only logarithmic in the number of points.
Up to a bilipschitz homeomorphism, the word metric depends only on the group and not on the chosen finite generating set.
This is particularly useful in computer science and discrete mathematics, where algorithms often perform more efficiently on simpler structures like tree metrics.
distortion bound has led to improved approximation ratios in several algorithmic problems, demonstrating the practical significance of this theoretical result.
Most notably, in functional analysis pseudometrics often come from seminorms on vector spaces, and so it is natural to call them "semimetrics".
Occasionally, a quasimetric is defined as a function that satisfies all axioms for a metric with the possible exception of symmetry.
This quasimetric describes the cost of modifying a metal stick: it is easy to reduce its size by filing it down, but it is difficult or impossible to grow it.
For example, the topology induced by the quasimetric on the reals described above is the (reversed) Sorgenfrey line.
Relaxing the last three axioms leads to the notion of a premetric, i.e. a function satisfying the following conditions: This is not a standard term.
Sometimes it is used to refer to other generalizations of metrics such as pseudosemimetrics[44] or pseudometrics;[45] in translations of Russian books it sometimes appears as "prametric".
Sets equipped with an extended pseudoquasimetric were studied by William Lawvere as "generalized metric spaces".