Gambler's fallacy

The fallacy leads to the incorrect notion that previous failures will create an increased probability of success on subsequent attempts.

However, it is a fallacy that a sequence of trials carries a memory of past results which tend to favor or disfavor future outcomes.

[2] An example of a retrospective gambler's fallacy would be to observe multiple successive "heads" on a coin toss and conclude from this that the previously unknown flip was "tails".

[3] Daniel M. Oppenheimer and Benoît Monin argue that "In other words, the 'best explanation' for a low-probability event is that it is only one in a multiple of trials, which is the core intuition of the reverse gambler's fallacy.

An example of the gambler's fallacy occurred in a game of roulette at the Monte Carlo Casino on August 18, 1913, when the ball fell in black 26 times in a row.

This was an extremely unlikely occurrence: the probability of a sequence of either red or black occurring 26 times in a row is (⁠18/37⁠)26-1 or around 1 in 66.6 million, assuming the mechanism is unbiased.

The opening scene of the play Rosencrantz and Guildenstern Are Dead by Tom Stoppard discusses these issues as one man continually flips heads and the other considers various possible explanations.

[11] Kahneman and Tversky interpret this to mean that people believe short sequences of random events should be representative of longer ones.

[12] The gambler's fallacy can also be attributed to the mistaken belief that gambling, or even chance itself, is a fair process that can correct itself in the event of streaks, known as the just-world hypothesis.

For events with a high degree of randomness, detecting a bias that will lead to a favorable outcome takes an impractically large amount of time and is very difficult, if not impossible, to do.

"[17] Human performance is not perceived as random, and people are more likely to continue streaks when they believe that the process generating the results is nonrandom.

A study by Huber, Kirchler, and Stockl in 2010 examined how the hot hand and the gambler's fallacy are exhibited in the financial market.

The researchers gave their participants a choice: they could either bet on the outcome of a series of coin tosses, use an expert opinion to sway their decision, or choose a risk-free alternative instead for a smaller financial reward.

Participants turned to the expert opinion to make their decision 24% of the time based on their past experience of success, which exemplifies the hot-hand.

This experiment helped bolster Ayton and Fischer's theory that people put more faith in human performance than they do in seemingly random processes.

[19] While the representativeness heuristic and other cognitive biases are the most commonly cited cause of the gambler's fallacy, research suggests that there may also be a neurological component.

Functional magnetic resonance imaging has shown that after losing a bet or gamble, known as riskloss, the frontoparietal network of the brain is activated, resulting in more risk-taking behavior.

These results suggest that gambler's fallacy relies more on the prefrontal cortex, which is responsible for executive, goal-directed processes, and less on the brain areas that control affective decision-making.

In individuals exhibiting the gambler's fallacy, this choice-outcome contingency method is impaired, and they continue to make risks after a series of losses.

The experimental group of participants was informed about the nature and existence of the gambler's fallacy, and were explicitly instructed not to rely on run dependency to make their guesses.

Fischbein and Schnarch theorized that an individual's tendency to rely on the representativeness heuristic and other cognitive biases can be overcome with age.

Participants exhibited the strongest gambler's fallacy when the seventh trial was part of the first block, directly after the sequence of three heads or tails.

They suggested that this would prevent people from gambling when they are losing, in the mistaken hope that their chances of winning are due to increase based on an interaction with previous events.

Within a real-world setting, numerous studies have uncovered that for various decision makers placed in high stakes scenarios, it is likely they will reflect some degree of strong negative autocorrelation in their judgement.

[25] Lottery play and jackpots entice gamblers around the globe, with the biggest decision for hopeful winners being what numbers to pick.

The key change in Terrell's study was the examination of a pari-mutuel lottery in which, a number selected with lower total wagers placed on it will result in a higher pay-out.

While this examination did conclude that players in both types of lotteries exhibited behaviour in-line with the gambler's fallacy theory, those who took part in pari-mutuel betting seemed to be less influenced.

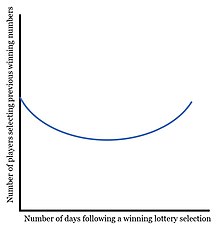
[26] The effect the of gambler's fallacy can be observed as numbers are chosen far less frequently soon after they are selected as winners, recovering slowly over a two-month period.

This is the gambler's fallacy in motion, as lottery players believe that the occurrence of a winning combination in previous days will decrease its likelihood of occurring today.

Several video games feature the use of loot boxes, a collection of in-game items awarded on opening with random contents set by rarity metrics, as a monetization scheme.