Hasse diagram
In order theory, a Hasse diagram (/ˈhæsə/; German: [ˈhasə]) is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction.
Such a diagram, with labeled vertices, uniquely determines its partial order.
One example that predates Hasse can be found in an 1895 work by Henri Gustave Vogt.
[2][3] Although Hasse diagrams were originally devised as a technique for making drawings of partially ordered sets by hand, they have more recently been created automatically using graph drawing techniques.
[4] In some sources, the phrase "Hasse diagram" has a different meaning: the directed acyclic graph obtained from the covering relation of a partially ordered set, independently of any drawing of that graph.
[5] Although Hasse diagrams are simple, as well as intuitive, tools for dealing with finite posets, it turns out to be rather difficult to draw "good" diagrams.
The reason is that, in general, there are many different possible ways to draw a Hasse diagram for a given poset.
The simple technique of just starting with the minimal elements of an order and then drawing greater elements incrementally often produces quite poor results: symmetries and internal structure of the order are easily lost.
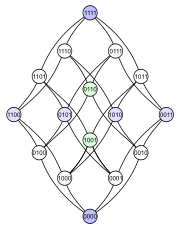
Each subset has a node labelled with a binary encoding that shows whether a certain element is in the subset (1) or not (0): The first diagram makes clear that the power set is a graded poset.
The second diagram has the same graded structure, but by making some edges longer than others, it emphasizes that the 4-dimensional cube is a combinatorial union of two 3-dimensional cubes, and that a tetrahedron (abstract 3-polytope) likewise merges two triangles (abstract 2-polytopes).
If a partial order can be drawn as a Hasse diagram in which no two edges cross, its covering graph is said to be upward planar.
A number of results on upward planarity and on crossing-free Hasse diagram construction are known: In software engineering / Object-oriented design, the classes of a software system and the inheritance relation between these classes is often depicted using a class diagram, a form of Hasse diagram in which the edges connecting classes are drawn as solid line segments with an open triangle at the superclass end.