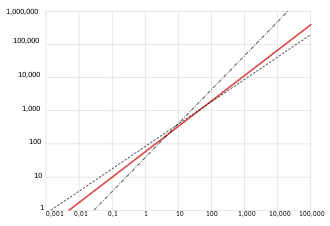
Kleiber's law
[5] Max Kleiber first discovered the law when analyzing a large number of independent studies on respiration within individual species.
Because many physiological processes, like heat loss and nutrient uptake, were believed to be dependent on the surface area of an organism, it was hypothesized that metabolic rate would scale with the 2/3 power of body mass.
Reasonable estimates for organisms' surface area do appear to scale linearly with the metabolic rate.
[9] West, Brown, and Enquist, (hereafter WBE) proposed a general theory for the origin of many allometric scaling laws in biology.
WBE claim that (1) metabolism should scale proportionally to nutrient flow (or, equivalently, total fluid flow) in this circulatory system and (2) in order to minimize the energy dissipated in transport, the volume of fluid used to transport nutrients (i.e., blood volume) is a fixed fraction of body mass.
[10] The model assumes that the energy dissipated is minimized and that the terminal tubes do not vary with body size.
It provides a complete analysis of numerous anatomical and physiological scaling relations for circulatory systems in biology that generally agree with data.
Thus, if B denotes the basal metabolic rate, Q the total fluid flow, and N the number of minimal tubules,
(Despite conceptual similarities, this condition is inconsistent with Murray's law)[12] Because blood volume is a fixed fraction of body mass,[10]
[10] Indeed, WBE predicts that the metabolic rates of the smallest animals tend to be greater than expected from the power-law scaling (see Fig.
[14] As a result, log-log plots of metabolic rate versus body mass can "curve" slightly upward, and fit better to quadratic models.
[16] Elaborations of the WBE model predict larger scaling exponents, worsening the discrepancy with observed data.
However, one can retain a similar theory by relaxing WBE's assumption of a nutrient transport network that is both fractal and circulatory.
[16] WBE argued that fractal-like circulatory networks are likely under strong stabilizing selection to evolve to minimize energy used for transport.
If selection for greater metabolic rates is favored, then smaller organisms will prefer to arrange their networks to scale as 2⁄3.
Still, selection for larger-mass organisms will tend to result in networks that scale as 3⁄4, which produces the observed curvature.
[21] The theoretical maximum value of f is 21%, because the efficiency of glucose oxidation is only 42%, and half of the ATP so produced is wasted.
[23] Other researchers have also noted that Kozłowski and Konarzewski's criticism of the law tends to focus on precise structural details of the WBE circulatory networks but that the latter are not essential to the model.
[27] The taxonomic level that body mass metabolic allometry should be studied has been debated [28][29] Nonetheless, several analyses suggest that while the exponents of the Kleiber's relationship between body size and metabolism can vary at the intraspecific level, statistically, intraspecific exponents in both plants and animals tend to cluster around 3/4.
[32] Similarly, a 2006 paper in Nature argued that the exponent of mass is close to 1 for plant seedlings, but that variation between species, phyla, and growth conditions overwhelm any "Kleiber's law"-like effects.