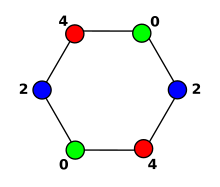
L(2,1)-coloring

In an L(2, 1)-coloring of a graph, G, the vertices of G are assigned color numbers in such a way that adjacent vertices get labels that differ by at least two, and the vertices that are at a distance of two from each other get labels that differ by at least one.

However, rather than counting the number of distinct colors used in an L(2,1)-coloring, research has centered on the L(2,1)-labeling number, the smallest integer

The L(2,1)-coloring problem was introduced in 1992 by Jerrold Griggs and Roger Yeh, motivated by channel allocation schemes for radio communication.

They proved that for cycles, such as the 6-cycle shown, the L(2,1)-labeling number is four, and that for graphs of degree

This graph theory-related article is a stub.