Vagueness
For example, the English adjective "tall" is vague since it is not clearly true or false for someone of middling height.
Vagueness is commonly diagnosed by a predicate's ability to give rise to the Sorites paradox.
), adulthood (most familiarly reflected in legal ages for driving, drinking, voting, consensual sex, etc.
The philosophical question of what the best theoretical treatment of vagueness is—which is closely related to the problem of the paradox of the heap, a.k.a.
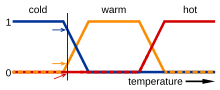
One theoretical approach is that of fuzzy logic, developed by American mathematician Lotfi Zadeh.
Fine argues that borderline applications of vague predicates are neither true nor false, but rather are instances of "truth value gaps".
This system has the consequence that borderline cases of vague terms yield statements that are neither true, nor false.
Since the presence of borderline cases seems to threaten principles like this one (excluded middle), the fact that supervaluationism can "rescue" them is seen as a virtue.
Subvaluationism is the logical dual of supervaluationism, and has been defended by Dominic Hyde (2008) and Pablo Cobreros (2011).
A fourth approach, known as "the epistemicist view", has been defended by Timothy Williamson (1994),[7] R. A. Sorensen (1988)[8] and (2001),[9] and Nicholas Rescher (2009).
This strategy has been poorly received, in part due to Gareth Evans's short paper "Can There Be Vague Objects?"
[11] Evans's argument appears to show that there can be no vague identities (e.g. "Princeton = Princeton Borough"), but as Lewis (1988) makes clear, Evans takes for granted that there are in fact vague identities, and that any proof to the contrary cannot be right.
[13] In the common law system, vagueness is a possible legal defence against by-laws and other regulations.
[15] The ability to cognition is the basic natural equipment of human (and other creatures) allowing him to orient and survive in the real (material) world.
Some information gained with less vagueness, others with greater one, according to the distance from the center (focus) of attention occupied by man during his act of cognition.
It is necessary to distinguish the internal cognitive model, i.e. the intrapsychic, stored and processed in human consciousness (and probably also in the unconscious), in hypothetical intrapsychic languages: imaginary, emotional and natural and in their mixture, and then the external model, represented in a suitable external language of communication.
Formal languages, mathematics, formal logic, programming languages (in principle, they must have zero internal vagueness of interpretation of all language constructs, i.e. they have exact interpretation) can model external vagueness by tools of vagueness and uncertainty representation: fuzzy sets and fuzzy logic, or by stochastic quantities and stochastic functions, as the exact sciences do.
In other cases cognitive model of certain part of real world may be simplified, such a way, that certain amount of deterministic information is possible to replace by fuzzy or stochastic one.
Demands on the accuracy of the formulation of scientific knowledge and its communication require minimizing the internal vagueness with which one connotes (vaguely, emotionally and subjectively interprets)[16] linguistic constructs of the communication language, and thus improve the accuracy of the message.
To formulate them, however, it is necessary to build a more precise language, with less (internal) vagueness of message than is common in daily life.
This is done by purposefully (branch) constructed terminology allowing to more accurately describe the researched reality and the acquired knowledge about it.
To improve the accuracy of research and communication (reducing the internal vagueness of connotation), tools such as classification schemes are used, such as the taxonomy of organisms by Carl von Linné.
The miraculous bridge between the real and exact worlds that makes this possible is called a quantity (e.g. electric field intensity, velocity, nitric acid concentration, etc.).
In exact sciences, it is always precisely defined, either consensually (basic set) or the other derived - International System of Units.
For every problem of the real world that is to be grasped by Newton’s method of the exact science, it is necessary to choose a group of suitable quantities, find the natural laws that apply in the real world between them, and describe them in mathematical language.
A group of selected quantities forms a discrete Newtonian filter (sieve) through which man ‘’look’’ at a given part of the real world.
Thus, in exact science, a given part of the real world is represented by a group of suitably chosen quantities and mathematically (programming language) described relations between them (more precisely between their names – symbols denoting them).
Even exact science needs to have a tool, with which it can describe the uncertainty of the results (obtained – knowledge), whether out of necessity or the need to abandon excessive precision.
Purely exact sciences, such as theoretical physics or mathematics, use natural language as meta-language.
The condition for the establishment of an exact science is to find suitable quantities, and this is possible only for a small part of the real world and for specific views of it.