Minifloat

This reduced precision makes them ill-suited for general-purpose numerical calculations, but they are useful for special purposes such as: Additionally, they are frequently encountered as a pedagogical tool in computer-science courses to demonstrate the properties and structures of floating-point arithmetic and IEEE 754 numbers.

Minifloats with 16 bits are half-precision numbers (opposed to single and double precision).

In this case they must obey the (not explicitly written) rules for the frontier between subnormal and normal numbers and must have special patterns for infinity and NaN.

and the exponent value is treated as 1 higher like the least normalized number: The significand is extended with "1.

": Infinity values have the highest exponent, with the mantissa set to zero.

There are only 242 different non-NaN values (if +0 and −0 are regarded as different), because 14 of the bit patterns represent NaNs.

At these small sizes other bias values may be interesting, for instance a bias of -2 will make the numbers 0-16 have the same bit representation as the integers 0-16, with the loss that no non-integer values can be represented.

A format could choose to give more of the bits to the exponent if they need more dynamic range with less precision, or give more of the bits to the significand if they need more precision with less dynamic range.

The exponent must be given at least one bit, or else it no longer makes sense as a float, it just becomes a signed number.

[6] Tables like the above can be generated for any combination of SEMB (sign, exponent, mantissa/significand, and bias) values using a script in Python or in GDScript.

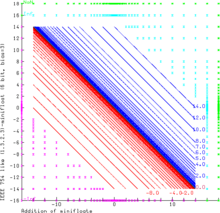
The range of the finite operands is filled with the curves x + y = c, where c is always one of the representable float values (blue and red for positive and negative results respectively).

Microsoft's D3D9 (Shader Model 2.0) graphics API initially supported both FP24 (as in ATI's R300 chip) and FP32 (as in Nvidia's NV30 chip) as "Full Precision", as well as FP16 as "Partial Precision" for vertex and pixel shader calculations performed by the graphics hardware.

If the mantissa is allowed to be 0-bit, a 1-bit float format would have a 1-bit exponent, and the only two values would be 0 and Inf.

The exponent must be at least 1 bit or else it no longer makes sense as a float (it would just be a signed number).

4-bit floating point numbers — without the four special IEEE values — have found use in accelerating large language models.

To speed up the computation, the mantissa typically occupies exactly half of the bits, so the register boundary automatically addresses the parts without shifting.