Non-neutral plasma
Due to unequal loss rates to the surface for electrons and ions, an electric field (the "ambipolar field") builds up, acting to hold back the more mobile species until the loss rates are the same.
The electrostatic potential (as measured in electron-volts) required to produce this electric field depends on many variables but is often on the order of the electron temperature.
They can be confined in a thermal equilibrium state using only static electric and magnetic fields, in a Penning trap configuration (see Fig.
[11] Using the "rotating wall" method,[12] the plasma confinement time can be increased arbitrarily.
If the temperature is sufficiently low (typically on the order of 10 mK), the plasma can become a non-neutral liquid or a crystal.
[9] Non-neutral plasmas with a single sign of charge can be confined for long periods of time using only static electric and magnetic fields.
Plasmas are confined in the axial direction by biasing the end electrodes so as to create an axial potential well that will trap charges of a given sign (the sign is assumed to be positive in the figure).
In the radial direction, confinement is provided by the v × B Lorentz force due to rotation of the plasma about the trap axis.
Mathematically, radial force balance implies a balance between electric, magnetic and centrifugal forces:[1] where m is particle mass, q is particle charge, r is radial distance from the trap axis and Er is the radial component of the electric field.
Depending on the radial electric field, the solutions for the rotation rate fall in the range
The slow and fast rotation modes meet when the electric field is such that
This is called the Brillouin limit; it is an equation for the maximum possible radial electric field that allows plasma confinement.
This radial electric field can be related to the plasma density n through the Poisson equation, and this equation can be used to obtain a relation between the density and the plasma rotation rate.
(1) implies that the radial electric field is proportional to radius r. Solving for Er from this equation in terms of
For a magnetic field of 10 tesla, the Brillouin density for electrons is only nB = 4.8×1014 cm−3.
(2), scaled by the Brillouin density, is shown as a function of rotation rate in Fig.
This rapid rotation is necessary to provide the confining radial Lorentz force for the plasma.
This loss process can be alleviated by operating the trap in an ultra high vacuum.
If these fields are not perfectly cylindrically symmetric, the asymmetries can torque on the plasma, reducing the rotation rate.
Such field errors are unavoidable in any actual experiment, and limit the plasma confinement time.
As a result, the system can access novel strongly coupled non-neutral states of matter, including plasma crystals consisting solely of a single charge species.
The coupling parameter can be thought of as the ratio of the mean interaction energy between nearest-neighbor pairs,
interactions between particles are important and the plasma behaves more like a liquid, or even a crystal if
In fact, computer simulations and theory have predicted that for an infinite homogeneous plasma the system exhibits a gradual onset of short-range order consistent with a liquid-like state for
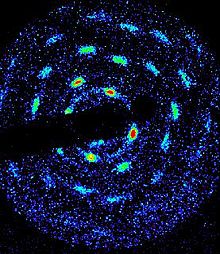
[10] Experiments have observed this crystalline state in a pure beryllium ion plasma that was laser-cooled to the millikelvin temperature range.
The mean inter-particle spacing in this pure ion crystal was on the order of 10-20 μm, much larger than in neutral crystalline matter.
This spacing corresponds to a density on the order of 108-109 cm−3, somewhat less than the Brillouin limit for beryllium in the 4.5 tesla magnetic field of the experiment.
The experiments measured the crystal structure by the Bragg-scattering technique, wherein a collimated laser beam was scattered off of the crystal, displaying Bragg peaks at the expected scattering angles for a bcc lattice (See Fig.
[9] When small numbers of ions are laser-cooled, they form crystalline "Coulomb clusters".
The symmetry of the cluster depends on the form of the external confinement fields.