Quadratic formula
Other ways of solving quadratic equations, such as completing the square, yield the same solutions.
satisfying the equation, called the roots or zeros, can be found using the quadratic formula,
written in terms of the coefficients; take the square root of both sides; and then isolate
The quadratic formula can equivalently be written using various alternative expressions, for instance
This variant has been jokingly called the "citardauq" formula ("quadratic" spelled backwards).
, subtraction can cause catastrophic cancellation, resulting in poor accuracy in numerical calculations; choosing between the version of the quadratic formula with the square root in the numerator or denominator depending on the sign of
This version of the quadratic formula is used in Muller's method for finding the roots of general functions.
Alternative methods are sometimes simpler than completing the square, and may offer interesting insight into other areas of mathematics.
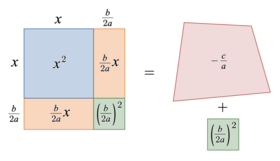
This method for completing the square is ancient and was known to the 8th–9th century Indian mathematician Śrīdhara.
[12] Compared with the modern standard method for completing the square, this alternate method avoids fractions until the last step and hence does not require a rearrangement after step 3 to obtain a common denominator in the right side.
Finally, after taking a square root of both sides and substituting the resulting expression for
The following method was used by many historical mathematicians:[13] Let the roots of the quadratic equation
An alternative way of deriving the quadratic formula is via the method of Lagrange resolvents,[14] which is an early part of Galois theory.
[15] This method can be generalized to give the roots of cubic polynomials and quartic polynomials, and leads to Galois theory, which allows one to understand the solution of algebraic equations of any degree in terms of the symmetry group of their roots, the Galois group.
This approach focuses on the roots themselves rather than algebraically rearranging the original equation.
Specific difficulties include catastrophic cancellation in computing the sum
[16][17] Catastrophic cancellation occurs when two numbers which are approximately equal are subtracted.
Therefore, naïvely following the standard quadratic formula often yields one result with less relative precision than expected.
Practical computer implementations of the solution of quadratic equations commonly choose which formula to use for each root depending on the sign of
[20] These methods do not prevent possible overflow or underflow of the floating-point exponent in computing
Babylonian cuneiform tablets contain problems reducible to solving quadratic equations.
[24] The Greek mathematician Euclid (circa 300 BC) used geometric methods to solve quadratic equations in Book 2 of his Elements, an influential mathematical treatise[25] Rules for quadratic equations appear in the Chinese The Nine Chapters on the Mathematical Art circa 200 BC.
[28] The Indian mathematician Brahmagupta included a generic method for finding one root of a quadratic equation in his treatise Brāhmasphuṭasiddhānta (circa 628 AD), written out in words in the style of the time but more or less equivalent to the modern symbolic formula.
The Indian mathematician Śrīdhara (8th–9th century) came up with a similar algorithm for solving quadratic equations in a now-lost work on algebra quoted by Bhāskara II.
[33] The 9th-century Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī solved quadratic equations algebraically.
[34] The quadratic formula covering all cases was first obtained by Simon Stevin in 1594.
[35] In 1637 René Descartes published La Géométrie containing special cases of the quadratic formula in the form we know today.
-axis, then the corresponding equation has a single repeated root on the line of symmetry, and this distance term is zero; algebraically, the discriminant
This can be a powerful tool for verifying that a quadratic expression of physical quantities has been set up correctly.
Fagnano, Giulio Carlo (1750), "Applicazione dell' algoritmo nuovo Alla resoluzione analitica dell' equazioni del secondo, del terzo, e del quarto grado" [Application of a new algorithm to the analytical resolution of equations of the second, third, and fourth degree], Produzioni matematiche del conte Giulio Carlo di Fagnano, Marchese de' Toschi, e DiSant' Ononio (in Italian), vol.