Quartz crystal microbalance

In liquid, it is highly effective at determining the affinity of molecules (proteins, in particular) to surfaces functionalized with recognition sites.

The piezoelectric effect has found applications in high power sources, sensors, actuators, frequency standards, motors, etc., and the relationship between applied voltage and mechanical deformation is well known; this allows probing an acoustic resonance by electrical means.

With an alternating current between the electrodes of a properly cut crystal, a standing shear wave is generated.

Common equipment allows resolution down to 1 Hz on crystals with a fundamental resonant frequency in the 4 – 6 MHz range.

A typical setup for the QCM contains water cooling tubes, the retaining unit, frequency sensing equipment through a microdot feed-through, an oscillation source, and a measurement and recording device.

As mass is deposited on the surface of the crystal, the thickness increases; consequently the frequency of oscillation decreases from the initial value.

[9] In the late 1980s, it was recognized that the QCM can also be operated in liquids, if proper measures are taken to overcome the consequences of the large damping.

The QCM measures inertial mass, and therefore by operating at a high resonant frequency it can be made very sensitive to small changes in that inertia as material is added to (or removed from) its surface.

The displacement pattern of an unloaded BAW resonator is a standing shear wave with anti-nodes at the crystal surface.

Grown crystals are subsequently cut and polished into hair-thin discs which support thickness shear resonance in the 1-30 MHz range.

Due to the piezo-effect, an AC voltage across the electrodes induces a shear deformation and vice versa.

The electromechanical coupling provides a simple way to detect an acoustic resonance by electrical means.

Compressional (longitudinal) waves would be radiated into the bulk and potentially be reflected back to the crystal from the opposing cell wall.

In impedance analysis, the electric conductance as a function of driving frequency is determined by means of a network analyzer.

This means that the mass-sensitivity is peaked at the center also, with this sensitivity declining smoothly to zero towards the rim (For high-frequency crystals, the amplitude vanishes already somewhat outside the perimeter of the smallest electrode.

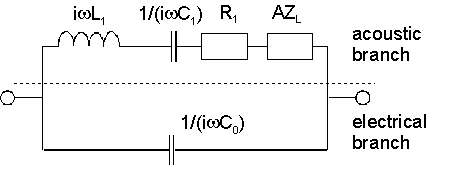
While φ is dimensionless for usual transformers (the turns ratio), it has the dimension charge/length in the case of electromechanical coupling.

[nb 1][43] Assume that the sample is a complex material, such as a cell culture, a sand pile, a froth, an assembly of spheres or vesicles, or a droplet.

If the average stress-to-speed ratio of the sample at the crystal surface (the load impedance, ZL) can be calculated in one way or another,[44] a quantitative analysis of the QCM experiment is in reach.

The limits of the small-load approximation are noticed either when the frequency shift is large or when the overtone-dependence of Δf and Δ(w/2) is analyzed in detail in order to derive the viscoelastic properties of the sample.

Angular brackets denote a time average and σ(t) is the (small) stress exerted by the external surface.

For a number of experimental configurations, there are explicit expressions relating the shifts of frequency and bandwidth to the sample properties.

The stress is governed by inertia, which implies σ = -ω2u0mF, where u0 is the amplitude of oscillation and mF is the (average) mass per unit area.

He simultaneously developed a method for measuring the resonance frequency and its changes by using the crystal as the frequency-determining component of an oscillator circuit.

His method continues to be used as the primary tool in quartz crystal microbalance experiments for conversion of frequency to mass.

Because the film is treated as an extension of thickness, Sauerbrey’s equation only applies to systems in which (a) the deposited mass has the same acoustic properties as the crystal and (b) the frequency change is small (Δf / f < 0.05).

Note that the properties of a film as determined with the QCM are fully specified by two parameters, which are its acoustic impedance, ZF = ρFcF and its mass per unit area, mF = dF/ρF.

However, if the correction factor differs significantly from unity, it may be expected that it affects the bandwidth Δ(w/2) and also that it depends on overtone order.

A "fluffy" interface will often lead to a viscoelastic correction and, as a consequence, to a non-zero Δ(w/2) as well as an overtone-dependent Sauerbrey mass.

The difference in dry and wet mass is shown with QCM-D and MP-SPR for instance in protein adsorption on nanocellulose[61][62] and in other soft materials.

A frequency shift is also induced when the crystal makes contact with discrete objects across small, load-bearing asperities.