Elastic pendulum
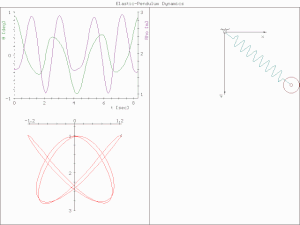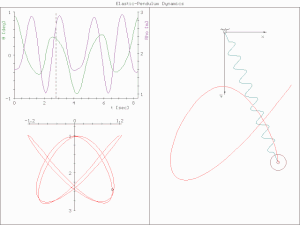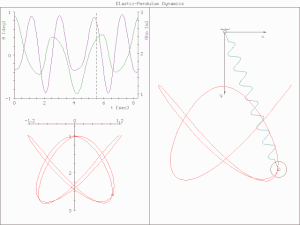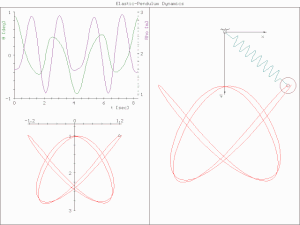
In physics and mathematics, in the area of dynamical systems, an elastic pendulum[1][2] (also called spring pendulum[3][4] or swinging spring) is a physical system where a piece of mass is connected to a spring so that the resulting motion contains elements of both a simple pendulum and a one-dimensional spring-mass system.
[2] For specific energy values, the system demonstrates all the hallmarks of chaotic behavior and is sensitive to initial conditions.
[2]At very low and very high energy, there also appears to be regular motion.
[5] The motion of an elastic pendulum is governed by a set of coupled ordinary differential equations.This behavior suggests a complex interplay between energy states and system dynamics.
The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system.
For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of angular momentum.
It is also possible that the spring has a range that is overtaken by the motion of the pendulum, making it practically neutral to the motion of the pendulum.
The spring has the rest length
The angle of oscillation of the pendulum is
Hooke's law is the potential energy of the spring itself: where
The potential energy from gravity, on the other hand, is determined by the height of the mass.
For a given angle and displacement, the potential energy is: where
to the other variables, the velocity is written as a combination of a movement along and perpendicular to the spring: So the Lagrangian becomes:[1] With two degrees of freedom, for
isolated: These can be further simplified by scaling length
Expressing the system in terms of
results in nondimensional equations of motion.
The one remaining dimensionless parameter
The elastic pendulum is now described with two coupled ordinary differential equations.
Furthermore, one can use analytical methods to study the intriguing phenomenon of order-chaos-order[7] in this system for various values of the parameter
There is also a second example : Double Elastic Pendulum .