Tensor (machine learning)
Data may be organized in a multidimensional array (M-way array), informally referred to as a "data tensor"; however, in the strict mathematical sense, a tensor is a multilinear mapping over a set of domain vector spaces to a range vector space.
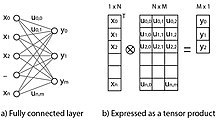
[1][6] Operations on data tensors can be expressed in terms of matrix multiplication and the Kronecker product.
[7] The computation of gradients, a crucial aspect of backpropagation, can be performed using software libraries such as PyTorch and TensorFlow.
These developments have greatly accelerated neural network architectures, and increased the size and complexity of models that can be trained.
Pierre Comon surveys the early adoption of tensor methods in the fields of telecommunications, radio surveillance, chemometrics and sensor processing.
Linear tensor rank methods (such as, Parafac/CANDECOMP) analyzed M-way arrays ("data tensors") composed of higher order statistics that were employed in blind source separation problems to compute a linear model of the data.
[10] In the early 2000s, multilinear tensor methods[1][11] crossed over into computer vision, computer graphics and machine learning with papers by Vasilescu or in collaboration with Terzopoulos, such as Human Motion Signatures,[12][13] TensorFaces[14][15] TensorTexures[16] and Multilinear Projection.
[17][18] Multilinear algebra, the algebra of higher-order tensors, is a suitable and transparent framework for analyzing the multifactor structure of an ensemble of observations and for addressing the difficult problem of disentangling the causal factors based on second order[14] or higher order statistics associated with each causal factor.
[19] When treating an image or a video as a 2- or 3-way array, i.e., "data matrix/tensor", tensor methods reduce spatial or time redundancies as demonstrated by Wang and Ahuja.
One of the early uses of tensors for neural networks appeared in natural language processing.
In 2009, the work of Sutskever introduced Bayesian Clustered Tensor Factorization to model relational concepts while reducing the parameter space.
[26][27] Lebedev et al. accelerated CNN networks for character classification (the recognition of letters and digits in images) by using 4D kernel tensors.
may be viewed as a 3rd order data tensor or 3-way array.-------- In natural language processing, a word might be expressed as a vector
Because a word is itself a vector, subject-object-verb semantics could be expressed using mode-3 tensors In practice the neural network designer is primarily concerned with the specification of embeddings, the connection of tensor layers, and the operations performed on them in a network.
Modern machine learning frameworks manage the optimization, tensor factorization and backpropagation automatically.
is the sum-product of its input units and the connection weights filtered through the activation function
A convolutional layer has multiple inputs, each of which is a spatial structure such as an image or volume.
The derivation is more complex when the filtering kernel also includes a non-linear activation function such as sigmoid or ReLU.
The work of Rabanser et al. provides an introduction to tensors with more details on the extension of Tucker decomposition to N-dimensions beyond the mode-3 example given here.
A tensor-train (TT) is a sequence of tensors of reduced rank, called canonical factors.
Developed in 2011 by Ivan Oseledts, the author observes that Tucker decomposition is "suitable for small dimensions, especially for the three-dimensional case.
This leads to new architectures, such as tensor-graph convolutional networks (TGCN), which identify highly non-linear associations in data, combine multiple relations, and scale gracefully, while remaining robust and performant.
[34][35][36][37] Tensors provide a unified way to train neural networks for more complex data sets.
[38] CUDA and thus cuDNN run on dedicated GPUs that implement unified massive parallelism in hardware.
These GPUs were not yet dedicated chips for tensors, but rather existing hardware adapted for parallel computation in machine learning.
[39] TPUs are dedicated, fixed function hardware units that specialize in the matrix multiplications needed for tensor products.
Specifically, they implement an array of 65,536 multiply units that can perform a 256x256 matrix sum-product in just one global instruction cycle.
The development of GPU hardware, combined with the unified architecture of tensor cores, has enabled the training of much larger neural networks.
In 2022, the largest neural network was Google's PaLM with 540 billion learned parameters (network weights)[43] (the older GPT-3 language model has over 175 billion learned parameters that produces human-like text; size isn't everything, Stanford's much smaller 2023 Alpaca model claims to be better,[44] having learned from Meta/Facebook's 2023 model LLaMA, the smaller 7 billion parameter variant).
The widely popular chatbot ChatGPT is built on top of GPT-3.5 (and after an update GPT-4) using supervised and reinforcement learning.