Velocity filter

[1][2] Many filtering techniques are available in which one output waveform is produced with a higher signal-to-noise ratio than the individual sensor recordings.

Without loss of generality, we shall assume that s0(t) is the desired signal and s1(t), s2(t), ..., sM(t) are the undesired interferences.

That is, By following the procedure discussed in Chen & Simaan (1990),[6][7] an optimum filter vector F(k) can be designed to attenuate, in the least square sense, the undesired coherent interferences S1(k), S2(k), ..., SM(k) while preserving the desired signal S0(k) in Y(k).

The multichannel processing scheme described by equations 6 to 10 produces one dimensional output trace.

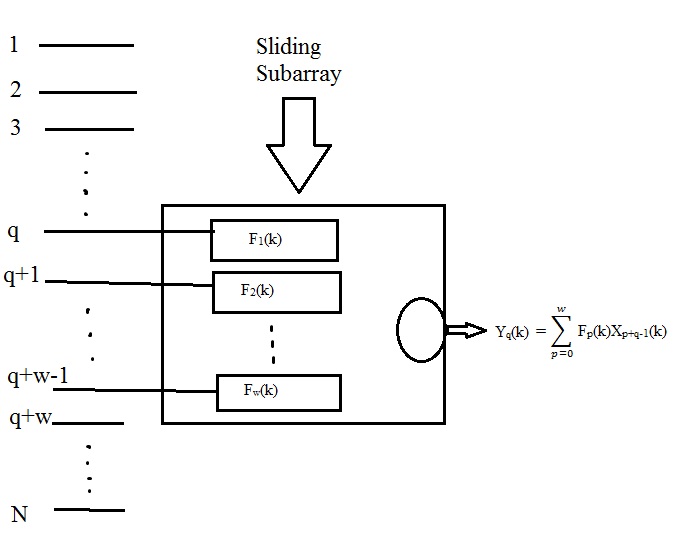
A two-dimensional record can be generated by a procedure which involves repeatedly applying multichannel optimum filters to a small number of overlapping subarrays of the input data,.

For every subarray position an optimum multichannel filter based on (9) can be designed so that the undesired interferences are suppressed from its corresponding output trace.

Clearly for such a scheme to work effectively W must be as small as possible; while at the same time it must be large enough to provide the necessary attenuation of the undesired signals.