Axial current
According to Noether's theorem, each symmetry of a system is associated a conserved quantity.
[1][2] For example, the rotational invariance of a system implies the conservation of its angular momentum, or spacetime invariance implies the conservation of energy–momentum.
In quantum field theory, internal symmetries also result in conserved quantities.
For example, the U(1) gauge transformation of QED implies the conservation of the electric charge.
Likewise, if a theory possesses an internal chiral or axial symmetry, there will be a conserved quantity, which is called the axial charge.
Further, just as the motion of an electrically charged particle produces an electric current, a moving axial charge constitutes an axial current.
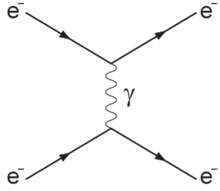
[3] For comparison, the electromagnetic current produced by an electrically charged moving particle is
As explained above, the axial current is simply the equivalent of the electromagnetic current for the axial symmetry instead of the U(1) symmetry.
Another perspective is given by recalling that the chiral symmetry is the invariance of the theory under the field rotation
Chiral symmetry is exhibited by vector gauge theories with massless fermions.
Since there is no known massless fermion in nature, chiral symmetry is at best an approximate symmetry in fundamental theories, and the axial current is not conserved.
(Note: this explicit breaking of the chiral symmetry by non-zero masses is not to be confused with the spontaneous chiral symmetry breaking that plays a dominant role in hadronic physics.)
An important consequence of such non-conservation is the neutral pion decay and the chiral anomaly,[4] which is directly related to the pion decay width.
[5][6] The axial current is an important part of the formalism describing high-energy scattering reactions.
The cross-section for such reaction is proportional to the square of the scattering amplitude, which in turn is given by the product of boson propagator times the two currents associated with the motions two colliding particles.
[7] Therefore, currents (axial or electromagnetic) are one of the two essential ingredients needed to compute high-energy scattering, the other being the boson propagator.
[8] (The spin-average part of the cross-section comes from the electromagnetic current.
[7]) In neutrino–nucleon scattering, neutrinos couple only via the axial current, thus accessing different nucleon structure information than with charged leptons.
[9] Neutral pions also couple only via the axial current because pions are pseudoscalar particles and, to produce amplitudes (scalar quantities), a pion must couple to another pseudoscalar object like the axial current.
(Charged pions can also couple via the electromagnetic current.)