Berman flow

In fluid dynamics, Berman flow is a steady flow created inside a rectangular channel with two equally porous walls.

The concept is named after a scientist Abraham S. Berman who formulated the problem in 1953.

[1] Consider a rectangular channel of width much longer than the height.

Let the distance between the top and bottom wall be

lies in the midway between the two walls, with

points perpendicular to the planes.

Let both walls be porous with equal velocity

Then the continuity equation and Navier–Stokes equations for incompressible fluid become[2] with boundary conditions The boundary conditions at the center is due to symmetry.

, the continuity equation dictates that the horizontal velocity

[3] Therefore, Berman introduced the following form, where

, that is to say This constant will be eliminated out of the problem and will have no influence on the solution.

this can substituted into the first equation after taking the derivative with respect to

Integrating once, we get with boundary conditions This third order nonlinear ordinary differential equation requires three boundary condition and the fourth boundary condition is to determine the constant

and this equation is found to possess multiple solutions.

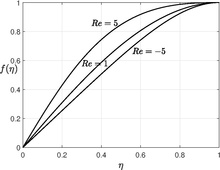
[4][5] The figure shows the numerical solution for low Reynolds number, solving the equation for large Reynolds number is not a trivial computation.

, the leading-order solution is given by[6] The above solution satisfies all the necessary boundary conditions even though Reynolds number is infinite (see also Taylor–Culick flow) The corresponding problem in porous pipe flows was addressed by S. W. Yuan and A. Finkelstein in 1955.