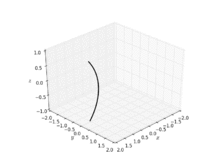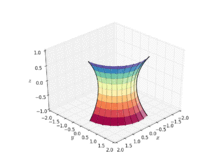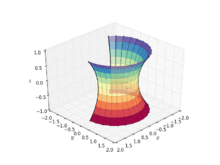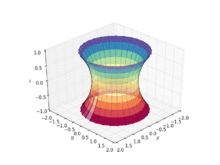
Catenoid

In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution).

[1] It is a minimal surface, meaning that it occupies the least area when bounded by a closed space.

Soap film attached to twin circular rings will take the shape of a catenoid.

[2] Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.

The catenoid was the first non-trivial minimal surface in 3-dimensional Euclidean space to be discovered apart from the plane.

The catenoid is obtained by rotating a catenary about its directrix.

[2] It was found and proved to be minimal by Leonhard Euler in 1744.

[3][4] Early work on the subject was published also by Jean Baptiste Meusnier.

[6] The catenoid may be defined by the following parametric equations:

A physical model of a catenoid can be formed by dipping two circular rings into a soap solution and slowly drawing the circles apart.

The catenoid may be also defined approximately by the stretched grid method as a facet 3D model.

Because they are members of the same associate family of surfaces, one can bend a catenoid into a portion of a helicoid without stretching.

In other words, one can make a (mostly) continuous and isometric deformation of a catenoid to a portion of the helicoid such that every member of the deformation family is minimal (having a mean curvature of zero).