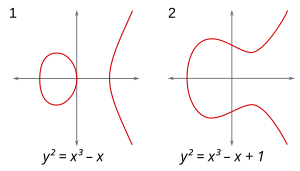
Harnack's curve theorem
For any algebraic curve of degree m in the real projective plane, the number of components c is bounded by The maximum number is one more than the maximum genus of a curve of degree m, attained when the curve is nonsingular.
Moreover, any number of components in this range of possible values can be attained.
A curve which attains the maximum number of real components is called an M-curve (from "maximum") – for example, an elliptic curve with two components, such as
or the Trott curve, a quartic with four components, are examples of M-curves.
This theorem formed the background to Hilbert's sixteenth problem.