History of calculus
Calculations of volumes and areas, one goal of integral calculus, can be found in the Egyptian Moscow papyrus (c. 1820 BC), but the formulas are only given for concrete numbers, some are only approximately true, and they are not derived by deductive reasoning.
[8] The method of exhaustion was independently invented in China by Liu Hui in the 4th century AD in order to find the area of a circle.
[10] In the Middle East, Hasan Ibn al-Haytham, Latinized as Alhazen (c. 965 – c. 1040 AD) derived a formula for the sum of fourth powers.
[11] Roshdi Rashed has argued that the 12th century mathematician Sharaf al-Dīn al-Tūsī must have used the derivative of cubic polynomials in his Treatise on Equations.
[13] Bhāskara also goes deeper into the 'differential calculus' and suggests the differential coefficient vanishes at an extremum value of the function, indicating knowledge of the concept of 'infinitesimals'.
But they did not combine many differing ideas under the two unifying themes of the derivative and the integral, show the connection between the two, and turn calculus into the powerful problem-solving tool we have today.
Torricelli extended Cavalieri's work to other curves such as the cycloid, and then the formula was generalized to fractional and negative powers by Wallis in 1656.
In the 17th century, European mathematicians Isaac Barrow, René Descartes, Pierre de Fermat, Blaise Pascal, John Wallis and others discussed the idea of a derivative.
In particular, in Methodus ad disquirendam maximam et minima and in De tangentibus linearum curvarum distributed in 1636, Fermat introduced the concept of adequality, which represented equality up to an infinitesimal error term.
The combination was achieved by John Wallis, Isaac Barrow, and James Gregory, the latter two proving predecessors to the second fundamental theorem of calculus around 1670.
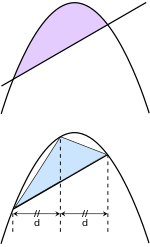
[24][25] James Gregory, influenced by Fermat's contributions both to tangency and to quadrature, was then able to prove a restricted version of the second fundamental theorem of calculus, that integrals can be computed using any of a function's antiderivatives.
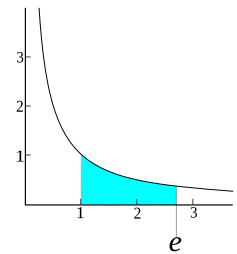
A. de Sarasa associated this feature with contemporary algorithms called logarithms that economized arithmetic by rendering multiplications into additions.
[32] Newton and Leibniz, building on this work, independently developed the surrounding theory of infinitesimal calculus in the late 17th century.
In comparison to the last century which maintained Hellenistic mathematics as the starting point for research, Newton, Leibniz and their contemporaries increasingly looked towards the works of more modern thinkers.
Newton succeeded in expanding the applicability of the binomial theorem by applying the algebra of finite quantities in an analysis of infinite series.
[35] Newton's formulated his calculus between the years 1664 to 1666,[36][37][38] later describing them as, "the prime of my age for invention and minded mathematics and [natural] philosophy more than at any time since."
It was during his plague-induced isolation that the first written conception of fluxionary calculus was recorded in the unpublished De Analysi per Aequationes Numero Terminorum Infinitas.
Particularly, his metaphysics which described the universe as a Monadology, and his plans of creating a precise formal logic whereby, "a general method in which all truths of the reason would be reduced to a kind of calculation".
By 1673 he had progressed to reading Pascal's Traité des sinus du quart de cercle and it was during his largely autodidactic research that Leibniz said "a light turned on".
From these definitions the inverse relationship or differential became clear and Leibniz quickly realized the potential to form a whole new system of mathematics.
Three hundred years after Leibniz's work, Abraham Robinson showed that using infinitesimal quantities in calculus could be given a solid foundation.
While neither of the two offered convincing logical foundations for their calculus according to mathematician Carl B. Boyer, Newton came the closest, with his best attempt coming in Principia, where he described his idea of "prime and ultimate ratios" and came extraordinarily close to the limit, and his ratio of velocities corresponded to a single real number, which would not be fully defined until the late nineteenth century.
Joseph Louis Lagrange contributed extensively to the theory, and Adrien-Marie Legendre (1786) laid down a method, not entirely satisfactory, for the discrimination of maxima and minima.
Other valuable treatises and memoirs have been written by Strauch (1849), Jellett (1850), Otto Hesse (1857), Alfred Clebsch (1858), and Carll (1885), but perhaps the most important work of the century is that of Karl Weierstrass.
Charles James Hargreave (1848) applied these methods in his memoir on differential equations, and George Boole freely employed them.
Niels Henrik Abel seems to have been the first to consider in a general way the question as to what differential equations can be integrated in a finite form by the aid of ordinary functions, an investigation extended by Liouville.
Frullani integrals, David Bierens de Haan's work on the theory and his elaborate tables, Lejeune Dirichlet's lectures embodied in Meyer's treatise, and numerous memoirs of Legendre, Poisson, Plana, Raabe, Sohncke, Schlömilch, Elliott, Leudesdorf and Kronecker are among the noteworthy contributions.
With its development are connected the names of Lejeune Dirichlet, Riemann, von Neumann, Heine, Kronecker, Lipschitz, Christoffel, Kirchhoff, Beltrami, and many of the leading physicists of the century.
Among them are the investigations of Euler on vibrating chords; Sophie Germain on elastic membranes; Poisson, Lamé, Saint-Venant, and Clebsch on the elasticity of three-dimensional bodies; Fourier on heat diffusion; Fresnel on light; Maxwell, Helmholtz, and Hertz on electricity; Hansen, Hill, and Gyldén on astronomy; Maxwell on spherical harmonics; Lord Rayleigh on acoustics; and the contributions of Lejeune Dirichlet, Weber, Kirchhoff, F. Neumann, Lord Kelvin, Clausius, Bjerknes, MacCullagh, and Fuhrmann to physics in general.
The labors of Helmholtz should be especially mentioned, since he contributed to the theories of dynamics, electricity, etc., and brought his great analytical powers to bear on the fundamental axioms of mechanics as well as on those of pure mathematics.