Incremental deformations
In solid mechanics, the linear stability analysis of an elastic solution is studied using the method of incremental deformations superposed on finite deformations.
[1] The method of incremental deformation can be used to solve static,[2] quasi-static [3] and time-dependent problems.
[4] The governing equations of the motion are ones of the classical mechanics, such as the conservation of mass and the balance of linear and angular momentum, which provide the equilibrium configuration of the material.
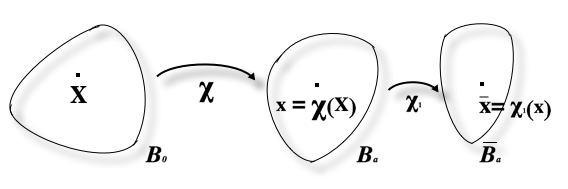
be two regions occupied by the material in two different instants of time.
Considering a hyperelastic material with an elastic strain energy density[5]
For a quasi-static problem, without body forces, the equilibrium equation is where
If the material is incompressible,[8] i.e. the volume of every subdomains does not change during the deformation, a Lagrangian multiplier[9] is typically introduced to enforce the internal isochoric constraint
depends nonlinearly[10] on the deformation gradient, this solution is generally not unique, and it depends on geometrical and material parameters of the problem.
So, one has to employ the method of incremental deformation in order to highlight the existence of an adjacent solution for a critical value of a dimensionless parameter, called control parameter
[11] This means that by increasing the value of this parameter, at a certain point new solutions appear.
Hence, the selected basic solution is not anymore the stable one but it becomes unstable.
In a physical way, at a certain time the stored energy, such as the integral of the density
[12] To improve this method, one has to superpose a small displacement
is the gradient operator with respect to the current configuration.
It is useful to derive the push-forward of the perturbed Piola stress be defined as where
is also known as the tensor of instantaneous moduli, whose components are: Expanding the equilibrium equation around the basic solution, one gets Since
is the divergence operator with respect to the actual configuration.
The incremental incompressibility constraint reads Expanding this equation around the basic solution, as before, one gets Let
represent the incremental boundary value problem (BVP) and define a system of partial differential equations (PDEs).
[13] The unknowns of the problem depend on the considered case.
For the first one, such as the compressible case, there are three unknowns, such as the components of the incremental deformations
The main difficulty to solve this problem is to transform the problem in a more suitable form for implementing an efficient and robusted numerical solution procedure.
It was originally developed by Stroh [15] for a steady state elastic problem and allows the set of four PDEs with the associated boundary conditions to be transformed into a set of ODEs of first order with initial conditions.
The number of equations depends on the dimension of the space in which the problem is set.
To do this, one has to apply variable separation and assume periodicity in a given direction depending on the considered situation.
[16] In particular cases, the system can be rewritten in a compact form by using the Stroh formalism.
is the only variable on which the rewritten problem depends and the matrix
[17] The Stroh formalism provides an optimal form to solve a great variety of elastic problems.
Optimal means that one can construct an efficient numerical procedure to solve the incremental problem.
By solving the incremental boundary value problem, one finds the relations[18] among the material and geometrical parameters of the problem and the perturbation modes by which the wave propagates in the material, i.e. what denotes the instability.