Quadratrix

Dinostratus, a Greek geometer and disciple of Plato, discussed the curve, and showed how it effected a mechanical solution of squaring the circle.

DAB is a quadrant in which the line DA and the arc DB are divided into the same number of equal parts.

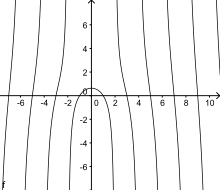
Letting A be the origin of the Cartesian coordinate system, D be the point (a, 0), a units from the origin along the x-axis, and B be the point (0, a), a units from the origin along the y-axis, the curve itself can be expressed by the equation[1] Because the cotangent function is invariant under negation of its argument, and has a simple pole at each multiple of π, the quadratrix has reflection symmetry across the y-axis, and similarly has a pole for each value of x of the form x = 2na, for integer values of n, except at x = 0 where the pole in the cotangent is canceled by the factor of x in the formula for the quadratrix.

These poles partition the curve into a central portion flanked by infinite branches.

The point where the curve crosses the y-axis has y = 2a/π; therefore, if it were possible to accurately construct the curve, one could construct a line segment whose length is a rational multiple of 1/π, leading to a solution of the classical problem of squaring the circle.

An accurate construction of the quadratrix would also allow the solution of two other classical problems known to be impossible with compass and straightedge: doubling the cube and trisecting an angle.

The quadratrix of Tschirnhaus[2] is constructed by dividing the arc and radius of a quadrant in the same number of equal parts as before.

Other curves that have historically been used to square the circle include the Archimedean spiral and the cochleoid.