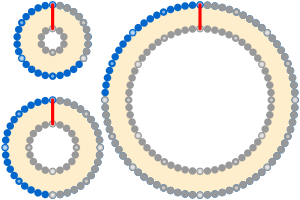
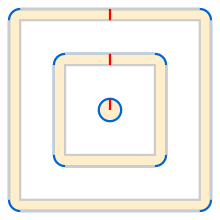
String girdling Earth

In a version of this puzzle, string is tightly wrapped around the equator of a perfectly spherical Earth.

The question that is then posed is whether the gap between string and Earth will allow the passage of a car, a cat or a thin knife blade.

The answer is that a cat will easily pass through the gap, the size of which will be ⁠1/2π ⁠ metres or about 16 cm (6.3 in).

Moreover, as in the coin-rolling problem, the shape the string girdles need not be a circle: 2π times the offset is added when it is any simple polygon or closed curve which does not intersect itself.

As aircraft fly at high altitude to save fuel due to lower drag, the formula shows that a Δa rise in altitude lengthens a flight along an entire great circle by 2π Δa.