Backpropagation through time

Backpropagation through time (BPTT) is a gradient-based technique for training certain types of recurrent neural networks, such as Elman networks.

The algorithm was independently derived by numerous researchers.

[1][2][3] The training data for a recurrent neural network is an ordered sequence of

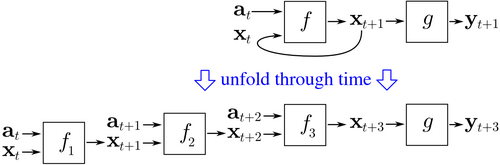
BPTT begins by unfolding a recurrent neural network in time.

inputs and outputs, but every copy of the network shares the same parameters.

Then, the backpropagation algorithm is used to find the gradient of the loss function with respect to all the network parameters.

Consider an example of a neural network that contains a recurrent layer

The cost of each time step can be computed separately.

The figure above shows how the cost at time

can be computed, by unfolding the recurrent layer

for three time steps and adding the feedforward layer

in the unfolded network shares the same parameters.

Below is pseudocode for a truncated version of BPTT, where the training data contains

input-output pairs, and the network is unfolded for

time steps: BPTT tends to be significantly faster for training recurrent neural networks than general-purpose optimization techniques such as evolutionary optimization.

[4] BPTT has difficulty with local optima.

With recurrent neural networks, local optima are a much more significant problem than with feed-forward neural networks.

[5] The recurrent feedback in such networks tends to create chaotic responses in the error surface which cause local optima to occur frequently, and in poor locations on the error surface.