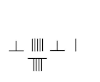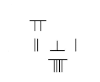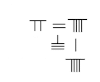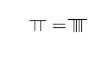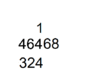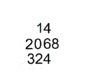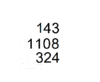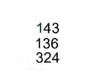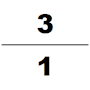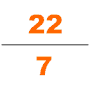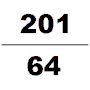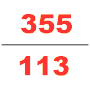Chinese mathematics

Since early times, Chinese understood basic arithmetic (which dominated far eastern history), algebra, equations, and negative numbers with counting rods.

However, the recent archaeological discovery of the Tsinghua Bamboo Slips, dated c. 305 BCE, has revealed some aspects of pre-Qin mathematics, such as the first known decimal multiplication table.

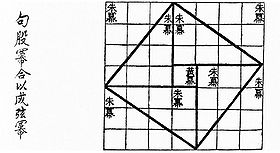
[13] The abacus was first mentioned in the second century BC, alongside 'calculation with rods' (suan zi) in which small bamboo sticks are placed in successive squares of a checkerboard.

Qin bamboo cash purchased at the antiquarian market of Hong Kong by the Yuelu Academy, according to the preliminary reports, contains the earliest epigraphic sample of a mathematical treatise.

The mathematical texts of the time, the Book on Numbers and Computation and Jiuzhang suanshu solved basic arithmetic problems such as addition, subtraction, multiplication and division.

[17] The Chinese did not focus on theoretical proofs based on geometry or algebra in the modern sense of proving equations to find area or volume.

Transcribing the problems directly from Yongle Encyclopedia, he then proceeded to make revisions to the original text, along with the inclusion his own notes explaining his reasoning behind the alterations.

[21] There is no explicit formula given within the text for the calculation of pi to be three, but it is used throughout the problems of both The Nine Chapters on the Mathematical Art and the Artificer's Record, which was produced in the same time period.

[27] Calculating the square and cube roots of numbers is done through successive approximation, the same as division, and often uses similar terms such as dividend (shi) and divisor (fa) throughout the process.

[20] There are a total of three sets of problems within The Book of Computations involving solving systems of equations with the false position method, which again are put into practical terms.

He discovered the usage of Cavalieri's principle to find an accurate formula for the volume of a cylinder, and also developed elements of the infinitesimal calculus during the 3rd century CE.

Khwarizmi's presentation is almost identical to the division algorithm in Sunzi, even regarding stylistic matters (for example, using blank spaces to represent trailing zeros); the similarity suggests that the results may not have been an independent discovery.

[31] Wang Xiaotong was a great mathematician in the beginning of the Tang dynasty, and he wrote a book: Jigu Suanjing (Continuation of Ancient Mathematics), where numerical solutions which general cubic equations appear for the first time.

[33][34] The table of sines by the Indian mathematician, Aryabhata, were translated into the Chinese mathematical book of the Kaiyuan Zhanjing, compiled in 718 AD during the Tang dynasty.

His book; Ceyuan haijing revolutionized the idea of inscribing a circle into triangles, by turning this geometry problem by algebra instead of the traditional method of using Pythagorean theorem.

Referring to Qin's solution of a 4th order equation, Yoshio Mikami put it: "Who can deny the fact of Horner's illustrious process being used in China at least nearly six long centuries earlier than in Europe?

[41] Pascal's triangle was first illustrated in China by Yang Hui in his book Xiangjie Jiuzhang Suanfa (詳解九章算法), although it was described earlier around 1050 by Jia Xian.

The Mathematical Treatise in Nine Sections, was written by the wealthy governor and minister Ch'in Chiu-shao (c. 1202 – c. 1261) and with the invention of a general method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.

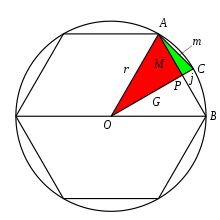
[48] Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry developed in the 13th century by the mathematician and astronomer Guo Shoujing (1231–1316).

[53]Correspondingly, scholars paid less attention to mathematics; preeminent mathematicians such as Gu Yingxiang and Tang Shunzhi appear to have been ignorant of the 'increase multiply' method.

In the late 16th century, Matteo Ricci decided to published Western scientific works in order to establish a position at the Imperial Court.

[57] However, contemporary scholars found the emphasis on proofs — as opposed to solved problems — baffling, and most continued to work from classical texts alone.

Meishi Congshu Jiyang was an encyclopedic summary of nearly all schools of Chinese mathematics at that time, but it also included the cross-cultural works of Mei Wending (1633–1721), Goucheng's grandfather.

[64] The long-missing mathematical works from Song and Yuan dynasties such as Si-yüan yü-jian and Ceyuan haijing were also found and printed, which directly led to a wave of new research.

[65] The most annotated works were Jiuzhang suanshu xicaotushuo (The Illustrations of Calculation Process for The Nine Chapters on the Mathematical Art ) contributed by Li Huang and Siyuan yujian xicao (The Detailed Explanation of Si-yuan yu-jian) by Luo Shilin.

[66] In 1840, the First Opium War forced China to open its door and look at the outside world, which also led to an influx of western mathematical studies at a rate unrivaled in the previous centuries.

Chinese scholars were initially unsure whether to approach the new works: was study of Western knowledge a form of submission to foreign invaders?

Some famous modern ethnic Chinese mathematicians include: In 1949, at the beginning of the founding of the People's Republic of China, the government paid great attention to the cause of science although the country was in a predicament of lack of funds.

In the field of mathematics, in addition to Chen Jingrun, Hua Luogeng, Zhang Guanghou and other mathematicians struggling to continue their work.

[74] An important mathematical achievement of the Chinese mathematician in the direction of the power system is how Xia Zhihong proved the Painleve conjecture in 1988.