Hilbert's eighth problem
Hilbert's eighth problem is one of David Hilbert's list of open mathematical problems posed in 1900.
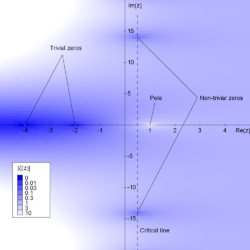
Hilbert calls for a solution to the Riemann hypothesis, which has long been regarded as the deepest open problem in mathematics.
Given the solution,[2] he calls for more thorough investigation into Riemann's zeta function and the prime number theorem.
Hilbert calls for a solution to the Goldbach conjecture, as well as more general problems, such as finding infinitely many pairs of primes solving a fixed linear diophantine equation.
Finally, Hilbert calls for mathematicians to generalize the ideas of the Riemann hypothesis to counting prime ideals in a number field.