[4] The LCP array was introduced in 1993, by Udi Manber and Gene Myers alongside the suffix array in order to improve the running time of their string search algorithm.

is a sentinel letter that is unique and lexicographically smaller than any other character.

denote the length of the longest common prefix between two strings

stores the length of longest common prefix of the lexicographically

is constructed by comparing lexicographically consecutive suffixes to determine their longest common prefix: So, for example,

Kärkkäinen & Sanders (2003) show that it is also possible to modify their

Assuming that each text symbol takes one byte and each entry of the suffix or LCP array takes 4 bytes, the major drawback of their algorithm is a large space occupancy of

Therefore, Manzini (2004) created a refined version of the algorithm of Kasai et al. (2001) (lcp9) and reduced the space occupancy to

Kärkkäinen, Manzini & Puglisi (2009) provide another refinement of Kasai's algorithm (

Rather than the actual LCP array, this algorithm builds the permuted LCP (PLCP) array, in which the values appear in text order rather than lexicographical order.

Gog & Ohlebusch (2011) provide two algorithms that although being theoretically slow (

As of 2012[update], the currently fastest linear-time LCP array construction algorithm is due to Fischer (2011), which in turn is based on one of the fastest suffix array construction algorithms (SA-IS) by Nong, Zhang & Chan (2009).

Fischer & Kurpicz (2017) based on Yuta Mori's DivSufSort is even faster.

As noted by Abouelhoda, Kurtz & Ohlebusch (2004) several string processing problems can be solved by the following kinds of tree traversals: Kasai et al. (2001) show how to simulate a bottom-up traversal of the suffix tree using only the suffix array and LCP array.

Abouelhoda, Kurtz & Ohlebusch (2004) enhance the suffix array with the LCP array and additional data structures and describe how this enhanced suffix array can be used to simulate all three kinds of suffix tree traversals.

Fischer & Heun (2007) reduce the space requirements of the enhanced suffix array by preprocessing the LCP array for range minimum queries.

[3] Abouelhoda, Kurtz & Ohlebusch (2004) show how to improve this running time even further to achieve optimal

It is sufficient to perform a linear scan through the LCP array in order to find its maximum value

The remainder of this section explains two applications of the LCP array in more detail: How the suffix array and the LCP array of a string can be used to construct the corresponding suffix tree and how it is possible to answer LCP queries for arbitrary suffixes using range minimum queries on the LCP array.

),[3] The issue with using standard binary search (without the LCP information) is that in each of the

comparisons needed to be made, we compare P to the current entry of the suffix array, which means a full string comparison of up to m characters.

, in the following way: At any point during the binary search algorithm, we consider, as usual, a range

, and decide whether we continue our search in the left sub-range

Another way of looking at it is : every entry of the suffix array occurs as central point of exactly one possible range during binary search.

that can possibly play a role during binary search, and it suffices to precompute

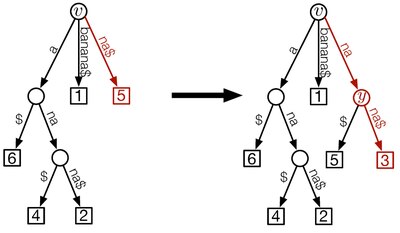
be the length of the concatenation of all path labels from the root of

, walk up the rightmost path beginning at the recently inserted leaf

We need to distinguish two cases: A simple amortization argument shows that the running time of this algorithm is bounded by

, it is possible to determine the length of the longest common prefix of arbitrary suffixes in

Therefore, the length of the longest prefix that is shared by all of these suffixes is the minimum value in the interval