Linearization
In mathematics, linearization (British English: linearisation) is finding the linear approximation to a function at a given point.
The linear approximation of a function is the first order Taylor expansion around the point of interest.
In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or discrete dynamical systems.
[1] This method is used in fields such as engineering, physics, economics, and ecology.
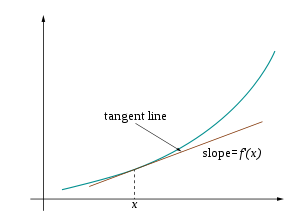
Linearizations of a function are lines—usually lines that can be used for purposes of calculation.
Linearization is an effective method for approximating the output of a function
based on the value and slope of the function at
In short, linearization approximates the output of a function near
The point-slope form of an equation forms an equation of a line, given a point
The general form of this equation is:
Because differentiable functions are locally linear, the best slope to substitute in would be the slope of the line tangent to
While the concept of local linearity applies the most to points arbitrarily close to
should be, most accurately, the slope of the tangent line at
Visually, the accompanying diagram shows the tangent line of
is any small positive or negative value,
The final equation for the linearization of a function at
The true value is close to 2.00024998, so the linearization approximation has a relative error of less than 1 millionth of a percent.
is: The general equation for the linearization of a multivariable function
[2] Linearization makes it possible to use tools for studying linear systems to analyze the behavior of a nonlinear function near a given point.
The linearization of a function is the first order term of its Taylor expansion around the point of interest.
In stability analysis of autonomous systems, one can use the eigenvalues of the Jacobian matrix evaluated at a hyperbolic equilibrium point to determine the nature of that equilibrium.
For time-varying systems, the linearization requires additional justification.
[3] In microeconomics, decision rules may be approximated under the state-space approach to linearization.
[4] Under this approach, the Euler equations of the utility maximization problem are linearized around the stationary steady state.
[4] A unique solution to the resulting system of dynamic equations then is found.
[4] In mathematical optimization, cost functions and non-linear components within can be linearized in order to apply a linear solving method such as the Simplex algorithm.
The optimized result is reached much more efficiently and is deterministic as a global optimum.
In multiphysics systems—systems involving multiple physical fields that interact with one another—linearization with respect to each of the physical fields may be performed.
This linearization of the system with respect to each of the fields results in a linearized monolithic equation system that can be solved using monolithic iterative solution procedures such as the Newton–Raphson method.
Examples of this include MRI scanner systems which results in a system of electromagnetic, mechanical and acoustic fields.