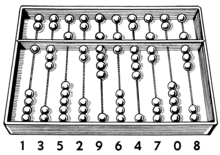
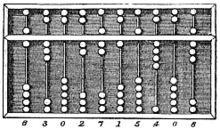
Abacus

Natural numbers are normally used, but some allow simple fractional components (e.g. 1⁄2, 1⁄4, and 1⁄12 in Roman abacus), and a decimal point can be imagined for fixed-point arithmetic.

The abacus has an advantage of not requiring a writing implement and paper (needed for algorism) or an electric power source.

Merchants, traders, and clerks in some parts of Eastern Europe, Russia, China, and Africa use abacuses.

The Latin word is derived from ancient Greek ἄβαξ (abax) which means something without a base, and colloquially, any piece of rectangular material.

[5][6][7] Alternatively, without reference to ancient texts on etymology, it has been suggested that it means "a square tablet strewn with dust",[8] or "drawing-board covered with dust (for the use of mathematics)"[9] (the exact shape of the Latin perhaps reflects the genitive form of the Greek word, ἄβακoς (abakos)).

[10][nb 1] Greek ἄβαξ probably borrowed from a Northwest Semitic language like Phoenician, evidenced by a cognate with the Hebrew word ʾābāq (אבק‎), or "dust" (in the post-Biblical sense "sand used as a writing surface").

He wrote that the Egyptians manipulated the pebbles from right to left, opposite in direction to the Greek left-to-right method.

[23] This Greek abacus was used in Achaemenid Persia, the Etruscan civilization, Ancient Rome, and the Western Christian world until the French Revolution.

It was covered with pictures, including a "treasurer" holding a wax tablet in one hand while manipulating counters on a table with the other.

[21] The normal method of calculation in ancient Rome, as in Greece, was by moving counters on a smooth table.

[25] One example of archaeological evidence of the Roman abacus, shown nearby in reconstruction, dates to the 1st century AD.

The Roman system of 'counter casting' was used widely in medieval Europe, and persisted in limited use into the nineteenth century.

In the long scroll Along the River During the Qingming Festival painted by Zhang Zeduan during the Song dynasty (960–1297), a suanpan is clearly visible beside an account book and doctor's prescriptions on the counter of an apothecary's (Feibao).

However, no direct connection has been demonstrated, and the similarity of the abacuses may be coincidental, both ultimately arising from counting with five fingers per hand.

Where the Roman model (like most modern Korean and Japanese) has 4 plus 1 bead per decimal place, the standard suanpan has 5 plus 2.

Another possible source of the suanpan is Chinese counting rods, which operated with a decimal system but lacked the concept of zero as a placeholder.

Later, Japan had a 3:5 abacus called 天三算盤, which is now in the Ize Rongji collection of Shansi Village in Yamagata City.

The use of the soroban is still taught in Japanese primary schools as part of mathematics, primarily as an aid to faster mental calculation.

Its use was taught in the Calmecac to the temalpouhqueh Nahuatl pronunciation: [temaɬˈpoʍkeʔ], who were students dedicated to taking the accounts of skies, from childhood.

The rediscovery of the Nepōhualtzintzin was due to the Mexican engineer David Esparza Hidalgo,[43] who in his travels throughout Mexico found diverse engravings and paintings of this instrument and reconstructed several of them in gold, jade, encrustations of shell, etc.

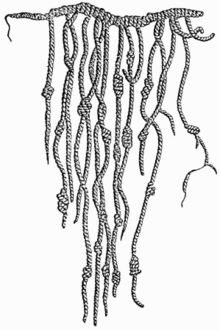
The quipu of the Incas was a system of colored knotted cords used to record numerical data,[45] like advanced tally sticks – but not used to perform calculations.

The working principle of a yupana is unknown, but in 2001 Italian mathematician De Pasquale proposed an explanation.

By comparing the form of several yupanas, researchers found that calculations were based using the Fibonacci sequence 1, 1, 2, 3, 5 and powers of 10, 20, and 40 as place values for the different fields in the instrument.

According to Yakov Perelman, some businessmen attempting to import calculators into the Russian Empire were known to leave in despair after watching a skilled abacus operator.

[50] Likewise, the mass production of Felix arithmometers since 1924 did not significantly reduce abacus use in the Soviet Union.

[52] The Russian abacus was brought to France around 1820 by mathematician Jean-Victor Poncelet, who had served in Napoleon's army and had been a prisoner of war in Russia.

[55] Around the world, abacuses have been used in pre-schools and elementary schools as an aid in teaching the numeral system and arithmetic.

People doing long-term AMC training show higher numerical memory capacity and experience more effectively connected neural pathways.

[60] AMC involves both visuospatial and visuomotor processing that generate the visual abacus and move the imaginary beads.

[62] The abacus shows how numbers, letters, and signs can be stored in a binary system on a computer, or via ASCII.