Euler angles
Alternative forms were later introduced by Peter Guthrie Tait and George H. Bryan intended for use in aeronautics and engineering in which zero degrees represent the horizontal position.
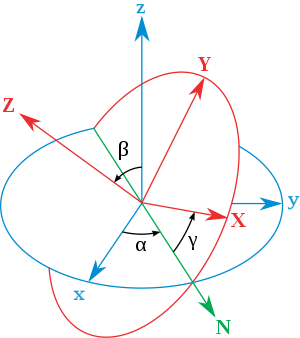
Euler angles are typically denoted as α, β, γ, or ψ, θ, φ.
The Euler or Tait–Bryan angles (α, β, γ) are the amplitudes of these elemental rotations.
For instance, the target orientation can be reached as follows (note the reversed order of Euler angle application): In sum, the three elemental rotations occur about z, x and z.
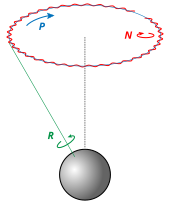
The six possible sequences are: Precession, nutation, and intrinsic rotation (spin) are defined as the movements obtained by changing one of the Euler angles while leaving the other two constant.
Only precession can be expressed in general as a matrix in the basis of the space without dependencies of the other angles.
The two in the middle work as two gimbal rings that allow the last frame to reach any orientation in space.
The second type of formalism is called Tait–Bryan angles, after Scottish mathematical physicist Peter Guthrie Tait (1831–1901) and English applied mathematician George H. Bryan (1864–1928).
Notice that this will not work if the rotations are applied in any other order or if the airplane axes start in any position non-equivalent to the reference frame.
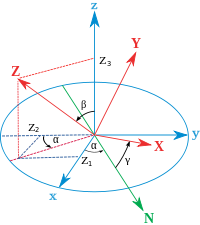
Here we present the results for the two most commonly used conventions: ZXZ for proper Euler angles and ZYX for Tait–Bryan.
, this leads to: and finally, using the inverse cosine function, Assuming a frame with unit vectors (X, Y, Z) given by their coordinates as in this new diagram (notice that the angle theta is negative), it can be seen that: As before, for
we have in a way analogous to the former one: Looking for similar expressions to the former ones: Note that the inverse sine and cosine functions yield two possible values for the argument.
This is because the sequence of rotations to reach the target frame is not unique if the ranges are not previously defined.
The following table contains formulas for angles α, β and γ from elements of a rotation matrix
[4] The Euler angles form a chart on all of SO(3), the special orthogonal group of rotations in 3D space.
A similar three angle decomposition applies to SU(2), the special unitary group of rotations in complex 2D space, with the difference that β ranges from 0 to 2π.
Other properties of Euler angles and rotations in general can be found from the geometric algebra, a higher level abstraction, in which the quaternions are an even subalgebra.
) It is possible to define parameters analogous to the Euler angles in dimensions higher than three.
Their main advantage over other orientation descriptions is that they are directly measurable from a gimbal mounted in a vehicle.
Therefore, gyros are used to know the actual orientation of moving spacecraft, and Euler angles are directly measurable.
The angular velocity of a rigid body takes a simple form using Euler angles in the moving frame.
Also the Euler's rigid body equations are simpler because the inertia tensor is constant in that frame.
In materials science, crystallographic texture (or preferred orientation) can be described using Euler angles.
[10] The most common definition of the angles is due to Bunge and corresponds to the ZXZ convention.
It is important to note, however, that the application generally involves axis transformations of tensor quantities, i.e. passive rotations.
Thus the matrix that corresponds to the Bunge Euler angles is the transpose of that shown in the table above.
Gun fire control systems require corrections to gun-order angles (bearing and elevation) to compensate for deck tilt (pitch and roll).
Gun mounts roll and pitch with the deck plane, but also require stabilization.
In quantum mechanics, explicit descriptions of the representations of SO(3) are very important for calculations, and almost all the work has been done using Euler angles.
In the early history of quantum mechanics, when physicists and chemists had a sharply negative reaction towards abstract group theoretic methods (called the Gruppenpest), reliance on Euler angles was also essential for basic theoretical work.