Quaternions and spatial rotation

Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space.

Rotation and orientation quaternions have applications in computer graphics,[1] computer vision, robotics,[2] navigation, molecular dynamics, flight dynamics,[3] orbital mechanics of satellites,[4] and crystallographic texture analysis.

However, they are not as intuitive and easy to understand and, due to the periodic nature of sine and cosine, rotation angles differing precisely by the natural period will be encoded into identical quaternions and recovered angles in radians will be limited to

Quaternions give a simple way to encode this [7] axis–angle representation using four real numbers, and can be used to apply (calculate) the corresponding rotation to a position vector (x,y,z), representing a point relative to the origin in R3.

gives 1, using the Taylor series of the exponential function, the extension of Euler's formula results: It can be shown[8] that the desired rotation can be applied to an ordinary vector

That fact is confirmed algebraically by noting that the conjugation is quadratic in q, so the sign of q cancels, and does not affect the result.

Mathematically, this operation carries the set of all "pure" quaternions p (those with real part equal to zero)—which constitute a 3-dimensional space among the quaternions—into itself, by the desired rotation about the axis u, by the angle θ.

This can be extended to arbitrary real n, allowing for smooth interpolation between spatial orientations; see Slerp.

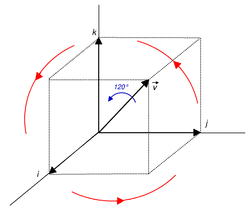
As a consequence, and This can be simplified, using the ordinary rules for quaternion arithmetic, to As expected, the rotation corresponds to keeping a cube held fixed at one point, and rotating it 120° about the long diagonal through the fixed point (observe how the three axes are permuted cyclically).

By using the formula for multiplication of two quaternions that are expressed as scalar and vector parts, this equation can be rewritten as where

Care should be taken when the quaternion approaches a scalar, since due to degeneracy the axis of an identity rotation is not well-defined.

Hamilton[12] presented the component form of these equations showing that the quaternion product computes the third vertex of a spherical triangle from two given vertices and their associated arc-lengths, which is also defines an algebra for points in Elliptic geometry.

The estimation of rotation angle is an essential procedure in 3D object registration or camera calibration.

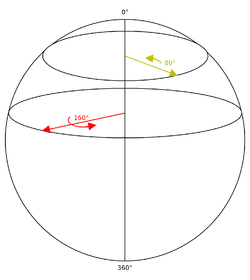
Continuing southward, the radii of the circles now become smaller (corresponding to the absolute value of the angle of the rotation considered as a negative number).

This behavior is matched by the set of unit quaternions: A general quaternion represents a point in a four dimensional space, but constraining it to have unit magnitude yields a three-dimensional space equivalent to the surface of a hypersphere.

A point (w, x, y) on the sphere represents a rotation in the ordinary space around the horizontal axis directed by the vector (x, y, 0) by an angle

Both dice are initially configured as shown in the upper left-hand corner (with 1 dot on the top face.)

), followed by a rotation about the +z axis, resulting in the configuration shown in the lower left corner (5 dots on the top face.)

This shows that, in general, the composition of two different rotations around two distinct spatial axes will not commute.

In quaternionic formalism the choice of an orientation of the space corresponds to order of multiplication: ij = k but ji = −k.

If one reverses the orientation, then the formula above becomes p ↦ q−1 p q, i.e., a unit q is replaced with the conjugate quaternion – the same behaviour as of axial vectors.

It is reported[16] that the existence and continued usage of an alternative quaternion convention in the aerospace and, to a lesser extent, robotics community is incurring a significant and ongoing cost [sic].

in [17] and departs from tradition by reversing the definition for multiplying quaternion basis elements such that under Shuster's convention,

Under Shuster's convention, the formula for multiplying two quaternions is altered such that The formula for rotating a vector by a quaternion is altered to be To identify the changes under Shuster's convention, see that the sign before the cross product is flipped from plus to minus.

In a gimbal-based aerospace inertial navigation system, for instance, this could have disastrous results if the aircraft is in a steep dive or ascent.

A more efficient calculation in which the quaternion does not need to be unit normalized is given by[20] where the following intermediate quantities have been defined: One must be careful when converting a rotation matrix to a quaternion, as several straightforward methods tend to be unstable when the trace (sum of the diagonal elements) of the rotation matrix is zero or very small.

Suppose, however, that we have some matrix Q that is not a pure rotation—due to round-off errors, for example—and we wish to find the quaternion q that most accurately represents Q.

In that case we construct a symmetric 4 × 4 matrix and find the eigenvector (x, y, z, w) corresponding to the largest eigenvalue (that value will be 1 if and only if Q is a pure rotation).

The quaternion so obtained will correspond to the rotation closest to the original matrix Q [dubious – discuss].

Likewise, angle–axis can be stored in a three-component vector by multiplying the unit direction by the angle (or a function thereof), but this comes at additional computational cost when using it for calculations.