Franck–Condon principle

Classically, the Franck–Condon principle is the approximation that an electronic transition is most likely to occur without changes in the positions of the nuclei in the molecular entity and its environment.

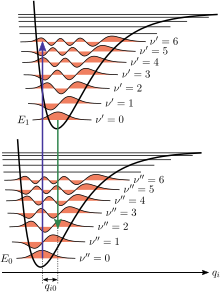
Figure 1 illustrates the Franck–Condon principle for vibronic transitions in a molecule with Morse-like potential energy functions in both the ground and excited electronic states.

The electron configuration of the new state may result in a shift of the equilibrium position of the nuclei constituting the molecule.

In the simplest case of a diatomic molecule the nuclear coordinates axis refers to the internuclear separation.

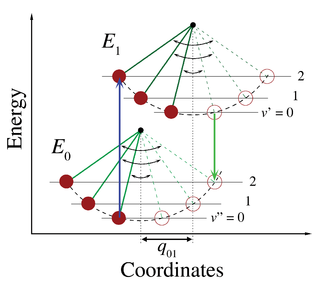
The applicability of the Franck–Condon principle in both absorption and fluorescence, along with Kasha's rule leads to an approximate mirror symmetry shown in Figure 2.

The vibrational structure of molecules in a cold, sparse gas is most clearly visible due to the absence of inhomogeneous broadening of the individual transitions.

Vibronic transitions are drawn in Figure 2 as narrow, equally spaced Lorentzian line shapes.

In a report published in 1926 in Transactions of the Faraday Society, James Franck was concerned with the mechanisms of photon-induced chemical reactions.

At the same time the equilibrium position of the nuclei moves with the excitation to greater values of r. If we go from the equilibrium position (the minimum of potential energy) of the n curve vertically [emphasis added] upwards to the a curves in Diagram I. the particles will have a potential energy greater than D' and will fly apart.

In this case we have a very great change in the oscillation energy on excitation by light...James Franck recognized that changes in vibrational levels could be a consequence of the instantaneous nature of excitation to higher electronic energy levels and a new equilibrium position for the nuclear interaction potential.

Edward Condon extended this insight beyond photoreactions in a 1926 Physical Review article titled "A Theory of Intensity Distribution in Band Systems".

The first joint reference to both Franck and Condon in regard to the new principle appears in the same 1926 issue of Physical Review in an article on the band structure of carbon monoxide by Raymond Birge.

Consider an electrical dipole transition from the initial vibrational state (υ) of the ground electronic level (ε),

Since the dependence is usually rather smooth it is neglected (i.e., the assumption that the transition dipole surface is independent of nuclear coordinates, called the Condon approximation is often allowed).

The remaining two integrals contributing to the probability amplitude determine the electronic spatial and spin selection rules.

Weaker magnetic dipole and electric quadrupole electronic transitions along with the incomplete validity of the factorization of the total wavefunction into nuclear, electronic spatial and spin wavefunctions means that the selection rules, including the Franck–Condon factor, are not strictly observed.

The table below gives the range of extinction coefficients for the possible combinations of allowed and forbidden spin and orbital selection rules.

However, this physical intuition can be, and is indeed, routinely extended to interactions between light-absorbing or emitting molecules (chromophores) and their environment.

Because the energy of single phonons is generally quite small, zero- or few-phonon transitions can only be observed at temperatures below about 40 kelvins.

The interaction itself involves electrostatic and van der Waals forces and can also include hydrogen bonds.

Franck–Condon principles can be applied when the interactions between the chromophore and the surrounding solvent molecules are different in the ground and in the excited electronic state.

This effect is analogous to the original Franck–Condon principle: the electronic transition is very fast compared with the motion of nuclei—the rearrangement of solvent molecules in the case of solvation.

When the solution is illuminated by light corresponding to the electronic transition energy, some of the chromophores will move to the excited state.

Since the electronic transition is essentially instantaneous on the time scale of solvent motion (vertical arrow), the collection of excited state chromophores is immediately far from equilibrium.

Note that while the electronic transitions are quantized, the chromophore-solvent interaction energy is treated as a classical continuum due to the large number of molecules involved.

Although emission is depicted as taking place from the minimum of the excited state chromophore-solvent interaction potential, significant emission can take place before equilibrium is reached when the viscosity of the solvent is high, or the lifetime of the excited state is short.

The energy difference between absorbed and emitted photons depicted in Figure 7 is the solvation contribution to the Stokes shift.

Figure 1. Franck–Condon principle energy diagram. Since electronic transitions are very fast compared with nuclear motions, the vibrational states to and from which absorption and emission occur are those that correspond to a minimal change in the nuclear coordinates. As a result, both absorption and emission produce molecules in vibrationally excited states . The potential wells are shown favoring transitions with changes in ν .
Figure 2. Schematic representation of the absorption and fluorescence spectra corresponding to the energy diagram in Figure 1. The symmetry is due to the equal shape of the ground and excited state potential wells. The narrow lines can usually only be observed in the spectra of dilute gases. The darker curves represent the inhomogeneous broadening of the same transitions as occurs in liquids and solids. Electronic transitions between the lowest vibrational levels of the electronic states (the 0–0 transition) have the same energy in both absorption and fluorescence.
Figure 3. Semiclassical pendulum analogy of the Franck–Condon principle. Vibronic transitions are allowed at the classical turning points because both the momentum and the nuclear coordinates correspond in the two represented energy levels. In this illustration, the 0–2 vibrational transitions are favored.
Figure 5. Figure 1 in Edward Condon's first publication on what is now the Franck–Condon principle [Condon 1926]. Condon chose to superimpose the potential curves to illustrate the method of estimating vibrational transitions.
Figure 6. Energy diagram of an electronic transition with phonon coupling along the configurational coordinate q i , a normal mode of the lattice. The upwards arrows represent absorption without phonons and with three phonons. The downwards arrows represent the symmetric process in emission.
Figure 7. Energy diagram illustrating the Franck–Condon principle applied to the solvation of chromophores. The parabolic potential curves symbolize the interaction energy between the chromophores and the solvent. The Gaussian curves represent the distribution of this interaction energy.