Gouy–Stodola theorem
It asserts that the rate at which work is lost during a process, or at which exergy is destroyed, is proportional to the rate at which entropy is generated, and that the proportionality coefficient is the temperature of the ambient heat reservoir.
[1] In the literature, the theorem often appears in a slightly modified form, changing the proportionality coefficient.
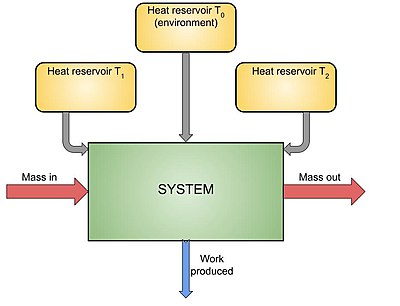
[5][6][7][8] The Gouy-Stodola theorem is often applied upon an open thermodynamic system, which can exchange heat with some thermal reservoirs.
The theorem, as stated above, holds only for the entire thermodynamic universe - the system along with its surroundings, together:
where the index "tot" denotes the total quantities produced within or by the entire universe.
[2] By integrating over the lifetime of the process, the theorem can also be expressed in terms of final quantities, rather than rates:
Similarly to the non-adiabatic case, the lost work is measured relative to some reference reservoir
Thus, this can be thought of as a special case of the above statement of the theorem - an adiabatic process is one for which the heat interactions with all reservoirs are zero, and in the reversible process, only the heat interaction with the reference thermal reservoir may be different.
During an irreversible process, such as heat exchanges with reservoirs, exergy is destroyed.
Unlike the lost work formulation, this version of the theorem holds for both the system (the control volume) and for its surroundings (the environment and the thermal reservoirs) separately:
where the index "sys" denotes quantities produced within or by the system itself, and "surr" within or by the surroundings.
where the index "tot" denotes the total quantities of the entire universe.
Thus, the exergy formulation of the theorem is less limited, as it can be applied on different regions separately.
The proof of the theorem, in both forms, uses the first law of thermodynamics, writing out the terms
In many cases, it is preferable to use a slightly modified version of the Gouy-Stodola theorem in work form, where
If both the pressure and the specific heat capacity remain constant, then the changes in enthalpy and entropy can be written in terms of the temperatures, and[2][11][12][13]
Specifically, in comparing the actual process to a reversible one, the modified version allows the final state to be different between the two.
This is in contrast to the original version, wherein reversible process is constructed to match so that the final states are the same.
[2][11] In general, the Gouy-Stodola theorem is used to quantify irreversibilities in a system and to perform exergy analysis.
That is, it allows one to take a thermodynamic system and better understand how inefficient it is (energy-wise), how much work is lost, how much room there is for improvement and where.
The second law of thermodynamics states, in essence, that the entropy of a system only increases.
Such a process may be steady, meaning that the matter and energy flowing into and out of the system are constant through time.
The theorem can help identify which components of a system have major irreversibilities, and how much exergy they destroy.
Overall, that is, the Gouy-Stodola theorem is a tool to find and quantify inefficiencies in a system, and can point to how to minimize them - this is the goal of exergy analysis.
An ecosystem is a complex system, where many factors and components interact, some biotic and some abiotic.
The Gouy-Stodola theorem can find how much entropy is generated by each part of the system, or how much work is lost.
Hence, two different states (for example, a healthy forest versus one which has undergone significant deforestation) of the same ecosystem may be compared in terms of entropy generation, and this may be used to evaluate the sustainability of the ecosystem under human interference.
They are rather complex systems, where many energy transformations occur, and they often waste heat.
Generally, the theorem may find applications in fields of biomedicine, or where biology and physics cross over, such as biochemical engineering thermodynamics.
[3][4][10] This is fundamentally different from most of the theorem's other uses - here, it isn't being applied in order to locate components with irreversibilities or loss of exergy, but rather helps give some more general information about the system.