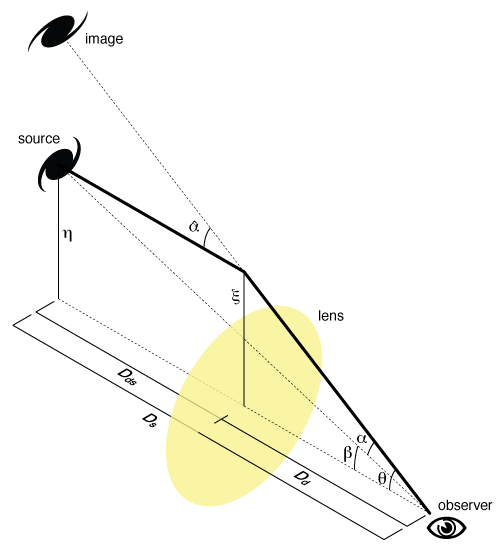
Gravitational lensing formalism

In general relativity, a point mass deflects a light ray with impact parameter

by an angle approximately equal to where G is the gravitational constant, M the mass of the deflecting object and c the speed of light.

A naive application of Newtonian gravity can yield exactly half this value, where the light ray is assumed as a massed particle and scattered by the gravitational potential well.

is the vector impact parameter of the actual ray path from the infinitesimal mass

The deflection angle is then As shown in the diagram on the right, the difference between the unlensed angular position

is this deflection angle, reduced by a ratio of distances, described as the lens equation where

In strong gravitational lensing, this equation can have multiple solutions, because a single source at

The term involving the convergence magnifies the image by increasing its size while conserving surface brightness.

The term involving the shear stretches the image tangentially around the lens, as discussed in weak lensing observables.

There is an alternative way of deriving the lens equation, starting from the photon arrival time (Fermat surface) where

The last can be obtained from the fact that a photon travels on a null geodesic of a weakly perturbed static Minkowski universe where the uneven gravitational potential

is so-called dimensionless time delay, and the 2D lensing potential The images lie at the extrema of this surface, so the variation of

for very small x we find One can compute the convergence by applying the 2D Laplacian of the 2D lensing potential in agreement with earlier definition

For a single point lens at the origin we recover the standard result that there will be two images at the two solutions of the essentially quadratic equation The amplification matrix can be obtained by double derivatives of the dimensionless time delay where we have define the derivatives which takes the meaning of convergence and shear.

In cases there are multiple point lenses plus a smooth background of (dark) particles of surface density

the time arrival surface is To compute the amplification, e.g., at the origin (0,0), due to identical point masses distributed at

we have to add up the total shear, and include a convergence of the smooth background, This generally creates a network of critical curves, lines connecting image points of infinite amplification.

In this case, the deflection can be derived by instead assuming that the gravitational potential is slowly varying everywhere (for this reason, this approximation is not valid for strong lensing).

This approach assumes the universe is well described by a Newtonian-perturbed FRW metric, but it makes no other assumptions about the distribution of the lensing mass.

As in the thin-lens case, the effect can be written as a mapping from the unlensed angular position

can be decomposed into convergence and shear terms just as with the thin-lens case, and in the limit of a lens that is both thin and weak, their physical interpretations are the same.

In weak gravitational lensing, the Jacobian is mapped out by observing the effect of the shear on the ellipticities of background galaxies.

In weak gravitational lensing, two different definitions are commonly used, and both are complex quantities which specify both the axis ratio and the position angle

: Like the traditional ellipticity, the magnitudes of both of these quantities range from 0 (circular) to 1 (a line segment).

The position angle is encoded in the complex phase, but because of the factor of 2 in the trigonometric arguments, ellipticity is invariant under a rotation of 180 degrees.

Image moments cannot generally be used to measure the ellipticity of galaxies without correcting for observational effects, particularly the point spread function.

, lensing generates an ellipse with major and minor axes as long as the shear and convergence do not change appreciably over the size of the source (in that case, the lensed image is not an ellipse).

Galaxies are not intrinsically circular, however, so it is necessary to quantify the effect of lensing on a non-zero ellipticity.

, so If we can assume that the sources are randomly oriented, their complex ellipticities average to zero, so This is the principal equation of weak lensing: the average ellipticity of background galaxies is a direct measure of the shear induced by foreground mass.

For a circularly symmetric lens, the magnification factor μ is given by In terms of convergence and shear For this reason, the Jacobian