Kaniadakis statistics

Kaniadakis statistics (also known as κ-statistics) is a generalization of Boltzmann–Gibbs statistical mechanics,[1] based on a relativistic[2][3][4] generalization of the classical Boltzmann–Gibbs–Shannon entropy (commonly referred to as Kaniadakis entropy or κ-entropy).

Introduced by the Greek Italian physicist Giorgio Kaniadakis in 2001,[5] κ-statistical mechanics preserve the main features of ordinary statistical mechanics and have attracted the interest of many researchers in recent years.

The κ-distribution is currently considered one of the most viable candidates for explaining complex physical,[6][7] natural or artificial systems involving power-law tailed statistical distributions.

Kaniadakis statistics have been adopted successfully in the description of a variety of systems in the fields of cosmology, astrophysics,[8][9] condensed matter, quantum physics,[10][11] seismology,[12][13] genomics,[14][15] economics,[16][17] epidemiology,[18] and many others.

Basic properties The κ-exponential function has the following properties of an exponential function: For a real number

, the κ-exponential has the property: The Kaniadakis logarithm (or κ-logarithm) is a relativistic one-parameter generalization of the ordinary logarithm function, with

, which is the inverse function of the κ-exponential: The κ-logarithm for

Basic properties The κ-logarithm function has the following properties of a logarithmic function: For a real number

, the Kaniadakis sum (or κ-sum) is defined by the following composition law: that can also be written in form: where the ordinary sum is a particular case in the classical limit

The κ-sum, like the ordinary sum, has the following properties: The κ-difference

arises as a special case of the more general expression below:

Furthermore, the κ-functions and the κ-sum present the following relationships: For any

, the Kaniadakis product (or κ-product) is defined by the following composition law: where the ordinary product is a particular case in the classical limit

The κ-product, like the ordinary product, has the following properties: The κ-division

arises as a special case of the more general expression below: The Kaniadakis differential (or κ-differential) of

The Kaniadakis integral (or κ-integral) is the inverse operator of the κ-derivative defined through which recovers the ordinary integral in the classical limit

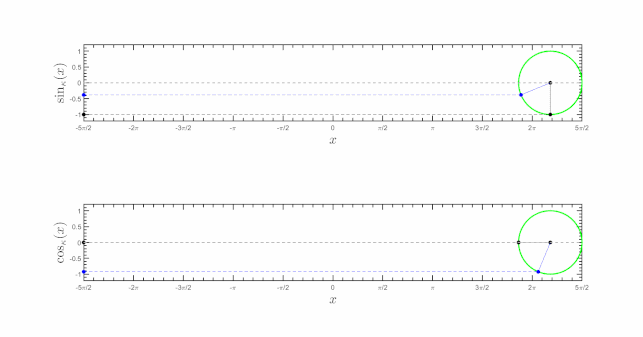
The Kaniadakis cyclic trigonometry (or κ-cyclic trigonometry) is based on the κ-cyclic sine (or κ-sine) and κ-cyclic cosine (or κ-cosine) functions defined by: where the κ-generalized Euler formula is The κ-cyclic trigonometry preserves fundamental expressions of the ordinary cyclic trigonometry, which is a special case in the limit κ → 0, such as: The κ-cyclic tangent and κ-cyclic cotangent functions are given by: The κ-cyclic trigonometric functions become the ordinary trigonometric function in the classical limit

κ-Inverse cyclic function The Kaniadakis inverse cyclic functions (or κ-inverse cyclic functions) are associated to the κ-logarithm: The Kaniadakis hyperbolic trigonometry (or κ-hyperbolic trigonometry) is based on the κ-hyperbolic sine and κ-hyperbolic cosine given by: where the κ-Euler formula is The κ-hyperbolic tangent and κ-hyperbolic cotangent functions are given by: The κ-hyperbolic trigonometric functions become the ordinary hyperbolic trigonometric functions in the classical limit

the fundamental expression of κ-hyperbolic trigonometry is given as follows: κ-Inverse hyperbolic function The Kaniadakis inverse hyperbolic functions (or κ-inverse hyperbolic functions) are associated to the κ-logarithm: in which are valid the following relations: The κ-cyclic and κ-hyperbolic trigonometric functions are connected by the following relationships: The Kaniadakis statistics is based on the Kaniadakis κ-entropy, which is defined through: where

is a probability distribution function defined for a random variable

The Kaniadakis κ-entropy is thermodynamically and Lesche stable[19][20] and obeys the Shannon-Khinchin axioms of continuity, maximality, generalized additivity and expandability.

A Kaniadakis distribution (or κ-distribution) is a probability distribution derived from the maximization of Kaniadakis entropy under appropriate constraints.

In this regard, several probability distributions emerge for analyzing a wide variety of phenomenology associated with experimental power-law tailed statistical distributions.

The κ-Laplace transform converts a function

, the following table presents the main properties of κ-Laplace transform:[21] The κ-Laplace transforms presented in the latter table reduce to the corresponding ordinary Laplace transforms in the classical limit

The κ-Fourier transform is defined as:[22] which can be rewritten as where

The κ-Fourier transform imposes an asymptotically log-periodic behavior by deforming the parameters

The inverse κ-Fourier transform is defined as:[22] Let

, the following table shows the κ-Fourier transforms of several notable functions:[22] The κ-deformed version of the Fourier transform preserves the main properties of the ordinary Fourier transform, as summarized in the following table.

The properties of the κ-Fourier transform presented in the latter table reduce to the corresponding ordinary Fourier transforms in the classical limit