Klee–Minty cube
The Klee–Minty cube or Klee–Minty polytope (named after Victor Klee and George J. Minty) is a unit hypercube of variable dimension whose corners have been perturbed.
Klee and Minty demonstrated that George Dantzig's simplex algorithm has poor worst-case performance when initialized at one corner of their "squashed cube".
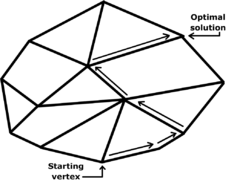
On the three-dimensional version, the simplex algorithm and the criss-cross algorithm visit all 8 corners in the worst case.
In 1973 Klee and Minty showed that Dantzig's simplex algorithm was not a polynomial-time algorithm when applied to their cube.
[2] The Klee–Minty cube was originally specified with a parameterized system of linear inequalities, with the dimension as the parameter.
Illustrations of the "cube" have appeared besides algebraic descriptions.
vertices, finally reaching the optimal vertex
The Klee–Minty cube has been used to analyze the performance of many algorithms, both in the worst case and on average.
The time complexity of an algorithm counts the number of arithmetic operations sufficient for the algorithm to solve the problem.
For example, Gaussian elimination requires the order of
For example, a generalization of Gaussian elimination called Buchberger's algorithm has for its complexity an exponential function of the problem data (the degree of the polynomials and the number of variables of the multivariate polynomials).
Because exponential functions eventually grow much faster than polynomial functions, an exponential complexity implies that an algorithm has slow performance on large problems.
In mathematical optimization, the Klee–Minty cube is an example that shows the worst-case computational complexity of many algorithms of linear optimization.
Klee and Minty showed that Dantzig's simplex algorithm visits all corners of a (perturbed) cube in dimension
[5] Modifications of the Klee–Minty construction showed similar exponential time complexity for other pivoting rules of simplex type, which maintain primal feasibility, such as Bland's rule.
[6] Another modification showed that the criss-cross algorithm, which does not maintain primal feasibility, also visits all the corners of a modified Klee–Minty cube.
[7] Like the simplex algorithm, the criss-cross algorithm visits all 8 corners of the three-dimensional cube in the worst case.
Further modifications of the Klee–Minty cube have shown the poor performance of central-path–following algorithms for linear optimization, in that the central path comes arbitrarily close to each of the corners of a cube.
This "vertex-stalking" performance is surprising because such path-following algorithms have polynomial-time complexity for linear optimization.
[8] The Klee–Minty cube has also inspired research on average-case complexity.
When eligible pivots are made randomly (and not by the rule of steepest descent), Dantzig's simplex algorithm needs on average quadratically many steps (on the order of
[9] Standard variants of the simplex algorithm take on average
[a] However according to Fukuda & Namiki (1994), when it is initialized at a random corner of the cube, the criss-cross algorithm visits only
[11] Both the simplex algorithm and the criss-cross algorithm visit exactly 3 additional corners of the three-dimensional cube on average.
The first two links have both an algebraic construction and a picture of a three-dimensional Klee–Minty cube: