UPGMA
UPGMA (unweighted pair group method with arithmetic mean) is a simple agglomerative (bottom-up) hierarchical clustering method.
It also has a weighted variant, WPGMA, and they are generally attributed to Sokal and Michener.
[1] Note that the unweighted term indicates that all distances contribute equally to each average that is computed and does not refer to the math by which it is achieved.
Thus the simple averaging in WPGMA produces a weighted result and the proportional averaging in UPGMA produces an unweighted result (see the working example).
[2] The UPGMA algorithm constructs a rooted tree (dendrogram) that reflects the structure present in a pairwise similarity matrix (or a dissimilarity matrix).
The UPGMA algorithm produces rooted dendrograms and requires a constant-rate assumption - that is, it assumes an ultrametric tree in which the distances from the root to every branch tip are equal.
When the tips are molecular data (i.e., DNA, RNA and protein) sampled at the same time, the ultrametricity assumption becomes equivalent to assuming a molecular clock.
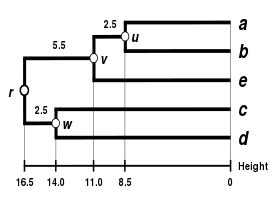
This working example is based on a JC69 genetic distance matrix computed from the 5S ribosomal RNA sequence alignment of five bacteria: Bacillus subtilis (
This corresponds to the expectation of the ultrametricity hypothesis.
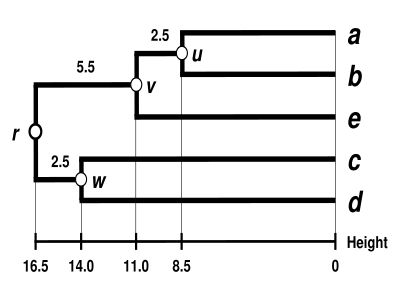
(see the final dendrogram) We then proceed to update the initial distance matrix
(see below), reduced in size by one row and one column because of the clustering of
are not affected by the matrix update as they correspond to distances between elements not involved in the first cluster.
We now reiterate the three previous steps, starting from the new distance matrix
Because of the ultrametricity constraint, the branches joining
We deduce the missing branch length:
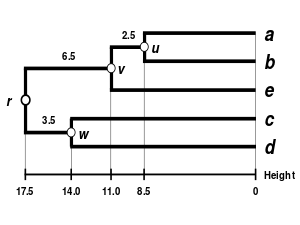
(see the final dendrogram) We then proceed to update
(see below), reduced in size by one row and one column because of the clustering of
correspond to the new distances, calculated by proportional averaging:
Thanks to this proportional average, the calculation of this new distance accounts for the larger size of the
cluster (two elements) with respect to
Proportional averaging therefore gives equal weight to the initial distances of matrix
This is the reason why the method is unweighted, not with respect to the mathematical procedure but with respect to the initial distances.
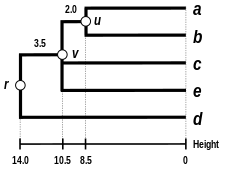
We again reiterate the three previous steps, starting from the updated distance matrix
(see the final dendrogram) There is a single entry to update, keeping in mind that the two elements
We deduce the two remaining branch lengths:
Implementing a different linkage is simply a matter of using a different formula to calculate inter-cluster distances during the distance matrix update steps of the above algorithm.
Complete linkage clustering avoids a drawback of the alternative single linkage clustering method - the so-called chaining phenomenon, where clusters formed via single linkage clustering may be forced together due to single elements being close to each other, even though many of the elements in each cluster may be very distant to each other.
Complete linkage tends to find compact clusters of approximately equal diameters.
[6] A trivial implementation of the algorithm to construct the UPGMA tree has
time complexity, and using a heap for each cluster to keep its distances from other cluster reduces its time to