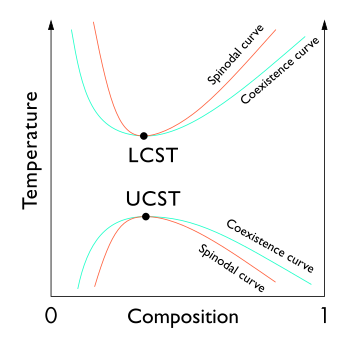Spinodal

In thermodynamics, the limit of local stability against phase separation with respect to small fluctuations is clearly defined by the condition that the second derivative of Gibbs free energy is zero.

[3] Inside it, only processes far from thermodynamic equilibrium, such as physical vapor deposition, will enable one to prepare single phase compositions.

[5] For binary solutions, the thermodynamic criterion which defines the spinodal curve is that the second derivative of free energy with respect to density or some composition variable is zero.

[7] The spinodal itself can be thought of as a line of pseudocritical points, with the correlation function taking a scaling form with non-classical critical exponents.

[10] In the case of ternary isothermal liquid-liquid equilibria, the spinodal curve (obtained from the Hessian matrix) and the corresponding critical point can be used to help the experimental data correlation process.